【標準】正接の加法定理と2直線のなす角
ここでは、 $\tan$ の加法定理を使って、2直線のなす角を求める問題を見ていきます。
2直線のなす角
【基本】三角関数の定義で見た通り、一般角の $\tan$ は傾きで定義します。これを逆に用いて、直線の傾きを考えるときに $\tan$ を利用する、という方法があります。
似たような話は三角比のところでも、【基本】三角比と2直線のなす角で扱っています。リンク先の問題では、傾きからすぐに角度がわかりましたが、 $\tan$ の加法定理を使えば、それぞれの角度がすぐにはわからない場合でも、2直線のなす角を考えられるようになります。
図は次のようになっています。
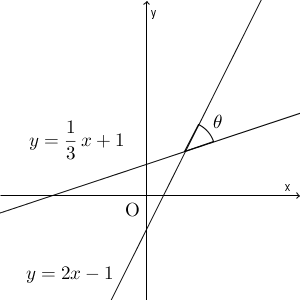
2直線のなす角をいきなり求めることは難しいですね。直線の方程式からわかることは、直線の傾き、つまり、直線と x 軸とのなす角についてだけです。これを用いて考えましょう。
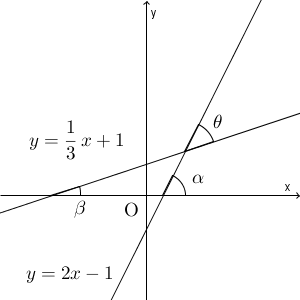
2直線と x 軸の正の向きとのなす角を、それぞれ $\alpha,\beta$ としましょう。傾きはどちらも正なので、どちらも鋭角としても構いません。求める $\theta$ は、 $\alpha-\beta$ で表すことができます。
$\alpha,\beta$ は、直接角度を求めることはできませんが、差の角の $\tan$ は求めることができます。\[ \tan\alpha=2, \tan\beta=\dfrac{1}{3} \]なので、加法定理を使って
\begin{eqnarray}
\tan\theta
&=&
\tan(\alpha-\beta) \\[5pt]
&=&
\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \\[5pt]
&=&
\frac{2-\frac{1}{3} }{1+2\times\frac{1}{3} } \\[5pt]
&=&
\frac{6-1}{3+2} \\[5pt]
&=&
1
\end{eqnarray}となります。よって、 $\tan\theta=\dfrac{\pi}{4}$ となることがわかります。
一般に、2つの直線 $y=a_1x+b_1$, $y=a_2x+b_2$ のなす角を $\theta$ とする( $\theta$ は鋭角)と、上と同様に考えて\[ \tan\theta=\left| \frac{a_1-a_2}{1+a_1a_2} \right| \]と書くことができます。
図形的に考える
先ほどの例題は、図形的に考えることもできます。2つの直線を、原点を通るように平行移動してもなす角は変わらないので、平行移動してから考えましょう。

ここで、それぞれの直線上にある点 $(1,2)$ と $(3,1)$ を考えます。この2点と原点とを結んでできる三角形は、辺の長さが $\sqrt{5}$, $\sqrt{5}$, $\sqrt{10}$ となります。このことから、この三角形は直角二等辺三角形となることがわかるので、2直線のなす角は45度、つまり $\dfrac{1}{4}\pi$ であることがわかります。
ただ、このようにうまい点を見つけて角度を考えることは難しいですね。こうした点を見つけなくても、直線の傾きを用いて、2直線のなす角の $\tan$ が求められる、というのは強力なツールであることがわかります。
おわりに
ここでは、 $\tan$ の加法定理を使用する例として、2直線のなす角を求める問題を見ました。2直線のなす角の $\tan$ は、加法定理を使えば求められる、ということをおさえておきましょう。





