【標準】三角関数の加法定理の証明

ここでは、三角関数の加法定理の証明を行っていきます。

余弦の加法定理

2つの角 $\alpha$ と $\beta$ の和の $\cos$ の値について考えます。

原点を O とし、点 $(1,0)$ を A とします。また、原点を中心として A を $\alpha+\beta$ だけ回転すると、点 P にうつるとします（回転は反時計回りが正の向き）。

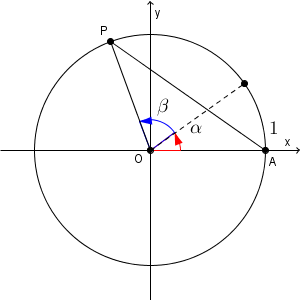
上の図では、どちらの角も正となっていますが、どんな角でも構いません。

さて、 P の座標は\[ (\cos(\alpha+\beta),\sin(\alpha+\beta)) \]なので、三平方の定理を使うと $\mathrm{ AP }^2$ は
\begin{eqnarray} & & (\cos(\alpha+\beta)-1)^2+\sin^2(\alpha+\beta) \\[5pt] &=& 2-2\cos(\alpha+\beta) \\[5pt] \end{eqnarray}となります。

また、この図全体を、原点を中心に $-\alpha$ だけ回転します。このとき、 A, P が、それぞれ、 $\mathrm{ A }'$, $\mathrm{ P }'$ に移動するとします。

$\mathrm{ A }'$ の座標は、負の角の式（参考：【基本】一般角の三角関数と鋭角の三角関数#マイナス角の三角関数）を使って\[ (\cos\alpha,-\sin\alpha) \]となります。また、 $\mathrm{ P }'$ の座標は $(\cos\beta,\sin\beta)$ なので、 $\mathrm{ A }'\mathrm{ P }'$ の長さの2乗は
\begin{eqnarray} & & (\cos\beta-\cos\alpha)^2+(\sin\beta+\sin\alpha)^2 \\[5pt] &=& 2-2\cos\beta\cos\alpha+2\sin\beta\sin\alpha \\[5pt] \end{eqnarray}となります。ここでも三平方の定理を使っています。

さて、回転移動をしても長さは変わらないので、 $\mathrm{ AP }$ と $\mathrm{ A }'\mathrm{ P }'$ は等しいから
\begin{eqnarray} 2-2\cos(\alpha+\beta) &=& 2-2\cos\beta\cos\alpha+2\sin\beta\sin\alpha \\[5pt] \cos(\alpha+\beta) &=& \cos\alpha\cos\beta-\sin\alpha\sin\beta \\[5pt] \end{eqnarray}となります。

また、 $\alpha,\beta$ はどんな角でもいいので、 $\beta$ のところを $-\beta$ としても構いません。よって、
\begin{eqnarray} \cos(\alpha-\beta) &=& \cos\alpha\cos(-\beta)-\sin\alpha(-\sin\beta) \\[5pt] &=& \cos\alpha\cos\beta+\sin\alpha\sin\beta \\[5pt] \end{eqnarray}が成り立ちます。

これらが、余弦の加法定理です。

正弦の加法定理

正弦の加法定理は、余弦の加法定理を利用して導きます。また、 $\dfrac{1}{2}\pi-\theta$ に関する式も用います。【標準】一般角の三角関数と鋭角の三角関数でも示しましたが、もう一度簡単に復習しておきましょう。

点 $(0,1)$ を、原点を中心にして、時計回りに $\theta$ だけ回転した点を考えます。これは、点 $(1,0)$ を、反時計回りに回転した場合で考えれば、 $\dfrac{1}{2}\pi-\theta$ だけ回転した点になります。

また、この点は $(1,0)$ を反時計回りに $\theta$ だけ回転した点と比べると $y=x$ について対称なので、 $x$ 座標と $y$ 座標が入れ替わります。このことから、 $\sin\left(\dfrac{1}{2}\pi-\theta\right)=\cos\theta$ と $\cos\left(\dfrac{1}{2}\pi-\theta\right)=\sin\theta$ が成り立ちます。

よって、この式を最初と最後に使い、余弦の加法定理も使うと
\begin{eqnarray} & & \sin(\alpha+\beta) \\[5pt] &=& \cos\left(\dfrac{1}{2}\pi-\alpha-\beta\right) \\[5pt] &=& \cos\left(\dfrac{1}{2}\pi-\alpha\right)\cos\beta+\sin\left(\dfrac{1}{2}\pi-\alpha\right)\sin\beta \\[5pt] &=& \sin\alpha\cos\beta+\cos\alpha\sin\beta \\[5pt] \end{eqnarray}となります。

また、余弦のときと同じで、 $\beta$ を $-\beta$ にすれば
\begin{eqnarray} \sin(\alpha-\beta) &=& \sin\alpha\cos(-\beta)+\cos\alpha\sin(-\beta) \\[5pt] &=& \sin\alpha\cos\beta-\cos\alpha\sin\beta \\[5pt] \end{eqnarray}となります。

これらが、正弦に関する加法定理です。

正接の加法定理

正接の加法定理は、余弦と正弦の加法定理を組み合わせて導くことができます。

相互関係より $\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ が成り立つので
\begin{eqnarray} & & \tan(\alpha+\beta) \\[5pt] &=& \dfrac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)} \\[5pt] &=& \dfrac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta} \\[5pt] &=& \dfrac{\frac{\sin\alpha}{\cos\alpha}+\frac{\sin\beta}{\cos\beta} }{1-\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta} } \\[5pt] &=& \dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \\[5pt] \end{eqnarray}が成り立ちます。

また、 $\beta$ を $-\beta$ とすれば
\begin{eqnarray} & & \tan(\alpha-\beta) \\[5pt] &=& \dfrac{\tan\alpha+\tan(-\beta)}{1-\tan\alpha\tan(-\beta)} \\[5pt] &=& \dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \\[5pt] \end{eqnarray}が得られます。

加法定理のまとめ

今までの内容をまとめると、次の式が成り立つことがわかりました。

おわりに

ここでは、三角関数の加法定理の証明を見てきました。余弦に関する加法定理から他の加法定理を導くことができます。【基本】図で理解する正弦・余弦の加法定理で見た内容とは異なり、ここでの内容は一般の角について成り立つ証明になっています。