【応用】三角関数の媒介変数表示を図形的に考えてみる
ここでは、半角の $\tan$ を用いた三角関数の媒介変数表示を、図形を使って考えていくことにします。
三角関数の媒介変数表示について
【応用】半角のtanを用いた三角関数の媒介変数表示でも見た通り、 $t=\tan\dfrac{1}{2}\theta$ とおいたとき、
\begin{eqnarray}
\sin\theta &=& \dfrac{2t}{1+t^2} \\[5pt]
\cos\theta &=& \dfrac{1-t^2}{1+t^2} \\[5pt]
\tan\theta &=& \dfrac{2t}{1-t^2} \\[5pt]
\end{eqnarray}と表されます。これらは、2倍角の定理を使って導けますが、 $t$ や $1+t^2$ などが図形的はどういうところから出てくるのだろう、というのを、考えていきます。ここで見る内容は知らなくても問題はありませんが、理解を深めるために見ていきます。
なお、使う図は、【応用】2倍角の公式を図形的に考えてみるで用いたものと同じです。角度の表記が少し違うだけです。
三角関数の媒介変数表示を図形的に考えてみる
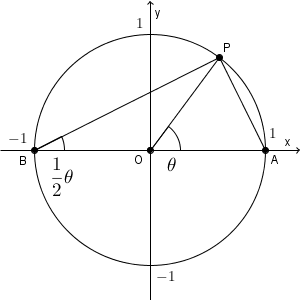
上の図のように、原点を $\mathrm{O}(0,0)$ とし、 $\mathrm{A}(1,0)$, $\mathrm{B}(-1,0)$ とします。また、原点を中心に点 A を反時計回りに $\theta$ だけ回転して移動する点を P とおきます。ただし、 $0\lt \theta \lt \dfrac{1}{2}\pi$ とします(ただ、他の場合も、長さの符号などを変えれば、以下と同様の議論ができます)。
媒介変数表示では、 $t=\tan\dfrac{1}{2}\theta$ とおきました。この $t$ は上の図のどこに出てくるかというと、 BP と y 軸とが交わるところですね。この点を Q とおくと、 $\mathrm{ Q }(0,t)$ となり、\[ \mathrm{ BO:OQ:QB } = 1:t:\sqrt{1+t^2} \]となります。

ここで、点 P から線分 AB に垂線を下ろし、その足を H とします。直角三角形 BPA と直角三角形 BOQ は相似なので、
\begin{eqnarray}
\mathrm{ BP:AB } &=& \mathrm{ BO:QB } \\[5pt]
&=& 1:\sqrt{1+t^2} \\[5pt]
\end{eqnarray}となることから、\[ \mathrm{ BP }=\dfrac{2}{\sqrt{1+t^2} } \]となります。さらに、直角三角形 BHP と直角三角形 BOQ も相似なので
\begin{eqnarray}
\mathrm{ BP:PH } &=& \mathrm{ BQ:QO } \\[5pt]
\dfrac{2}{\sqrt{1+t^2} }:\mathrm{ PH } &=& \sqrt{1+t^2}:t \\[5pt]
\mathrm{ PH } &=& \frac{2t}{1+t^2}
\end{eqnarray}となります。この PH の長さが $\sin\theta$ なので、\[ \sin\theta=\frac{2t}{1+t^2} \]と表されることがわかります。 $1+t^2$ というのは、 $1:t:\sqrt{1+t^2}$ という直角三角形の斜辺の2乗が出ていた、と考えることができるわけですね。

さらに、 $\cos\theta$ は、 $\mathrm{ BH-OH }$ とかけます。 BH は
\begin{eqnarray}
\mathrm{ BP:BH } &=& \mathrm{ BQ:BO } \\[5pt]
\dfrac{2}{\sqrt{1+t^2} }:\mathrm{ BH } &=& \sqrt{1+t^2}:1 \\[5pt]
\mathrm{ PH } &=& \frac{2}{1+t^2}
\end{eqnarray}なので、
\begin{eqnarray}
\cos\theta
&=&
\frac{2}{1+t^2} -1 \\[5pt]
&=&
\frac{1-t^2}{1+t^2}
\end{eqnarray}となります。 $\tan\theta$ は相互関係から $\tan\theta=\dfrac{2t}{1-t^2}$ となりますね。
このようにして、媒介変数表示を図形的に考えることができます。
おわりに
ここでは、 $\tan\dfrac{1}{2}\theta$ から $\sin\theta$, $\cos\theta$, $\tan\theta$ を表す方法を、図形的に考えてみました。円周角の定理が使える図を用い、線分の長さに注目すれば求めることができます。この内容は、一般的な「媒介変数表示」を学ぶときにもう一度見ることになるでしょう。





