【応用】半角の公式を図形的に考えてみる

🕒 2019/03/18 🔄 2023/05/01

ここでは、二等辺三角形を用いて、半角の公式を図形的に考えてみることにします。ここの内容は、正式な証明ではなく、知らなくても問題ないのですが、理解を深めるために見ていきます。

📘 目次

半角の公式を図形的に考える準備

【標準】半角の公式で見たように、半角の公式は、次のような内容でした。
\begin{eqnarray} \sin^2 \dfrac{\alpha}{2} &=& \frac{1-\cos \alpha}{2} \\[5pt] \cos^2 \dfrac{\alpha}{2} &=& \frac{1+\cos \alpha}{2} \\[5pt] \end{eqnarray}$\tan$ もありますが、ここでは、この2つについて取り上げます。

ここで、 $\mathrm{ AB=AC }=1$ で、 $\angle \mathrm{ A }=\alpha$ の二等辺三角形を考えてみましょう。

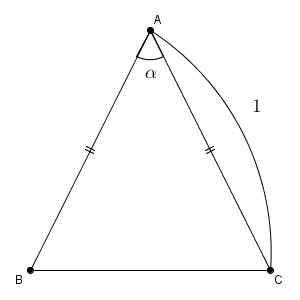
辺 BC の中点を M とすれば、 $\angle \mathrm{ BAM }=\dfrac{\alpha}{2}$ となりますね。

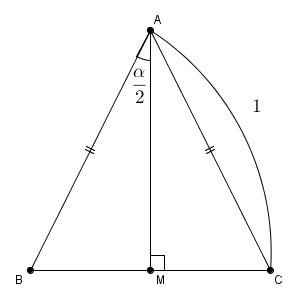
このことから、 $\mathrm{ AM }=\cos\dfrac{\alpha}{2}$ $\mathrm{ BM }=\sin\dfrac{\alpha}{2}$ が成り立つことがわかります。さらに、 M から辺 AB に垂線を下ろして、辺 AB と交わる点を P としましょう。

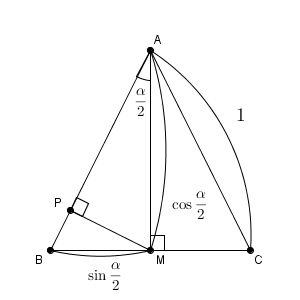
こうすると、三角形 AMP で考えれば、 AP の長さが $\cos^2\dfrac{\alpha}{2}$ となることがわかります。これは、半角の公式で出てきたものですね。

続いて、この図のどこに $\sin^2\dfrac{\alpha}{2}$ があらわれているかを考えてみましょう。 $\angle \mathrm{ BAM }$ も $\angle \mathrm{ BMP }$ も、 $\angle \mathrm{ AMP }$ を足せば90度なので、 $\angle \mathrm{ BMP }=\angle \mathrm{ BAM }=\dfrac{\alpha}{2}$ となることがわかります。よって、三角形 BMP で考えれば、 BP の長さが $\sin^2\dfrac{\alpha}{2}$ であることがわかります。

半角の $\sin, \cos$ の2乗が出てきました。これを $\alpha$ で表すとどうなるかを見ていきましょう。

半角の公式を図形的に考える

現時点での図をおさらいしておきましょう。 $\mathrm{ AB=AC }=1$ で、 $\angle \mathrm{ A }=\alpha$ の二等辺三角形を考え、 BC の中点を M とし、 M から AB に下した垂線の足を P としたのでした。

このとき、 AP, BP は、それぞれ、 $\cos^2\dfrac{\alpha}{2}$, $\sin^2\dfrac{\alpha}{2}$ となるのでしたね。

ここで、少し視点を変えて、 C から AB に下した垂線を考えてみましょう。 AB との交点を Q とすると、 AQ は $\cos\alpha$ になるので、 BQ の長さは $1-\cos\alpha$ となります。半角の公式が見えてきましたね。

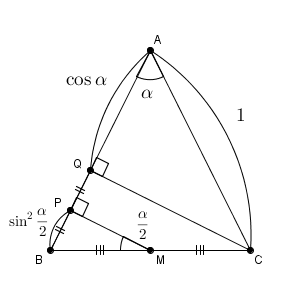
また、 MP と CQ は平行で、 $\mathrm{ BM=CM }$ なので、 $\mathrm{ BP=PQ }$ が成り立ちます。 $\sin^2\dfrac{\alpha}{2}$ は、 BP の長さだったので、BQ の半分だから\[ \sin^2\dfrac{\alpha}{2}=\dfrac{1-\cos\alpha}{2} \]となることがわかります。

$\cos^2\dfrac{\alpha}{2}$ は、 AP の長さでした。これは、 AQ に、 BQ の半分を足せばいいので
\begin{eqnarray} \cos^2\dfrac{\alpha}{2} &=& \cos\alpha+\frac{1-\cos\alpha}{2} \\[5pt] &=& \frac{1+\cos\alpha}{2} \end{eqnarray}となります（もちろん、 $1-\sin^2\dfrac{\alpha}{2}$ と考えて計算しても構いません）。

こうして、2つの半角の公式が得られました。