【発展】自然対数とガチャ(くじが当たらない確率)
ここでは、自然対数に絡んだ話題として、ガチャについて、もしくは「くじ」について考えていきます。
一回も当たらない確率
友人と2人でじゃんけんをして自分が勝つ確率は、理論的には50%だと考えられます。また、経験上わかると思いますが、2回じゃんけんをしたからといって、一勝一敗になるとは限りません。二勝することもあれば、二敗することもあります。つまり、一度も勝てないこともありえます。
ただ、スマホゲームで、レアアイテムをゲットするために「くじ」を引く(いわゆる「ガチャ」)とき、1%の出現確率であれば、100回引けば必ず当たる、と考えてしまう人がいます。
くじの数が100個で、当たりが1個含まれている、くじを引けばくじが減っていく、という状況なら、たしかに100回引けば必ず当たります。1回目で当たる確率は $\dfrac{1}{100}$ です。1回目で外れた場合、2回目に引くときには、くじが減っているので、当たる確率は $\dfrac{1}{99}$ となります。何度も外れた場合、次で当たる確率はどんどん高まり、99回はずれた場合、次で当たる確率は $1$ となります。
しかし、くじを引くたびに確率が初期状態に戻る場合は違います。一般的に、「ガチャ」で1回目で外れた場合、2回目の挑戦のときには、当たる確率は $\dfrac{1}{100}$ のままです。先ほどと違って、はずれくじが減っていくわけではありません。なので、100回引いても、必ず当たるわけではありません。
それでは、一度も当たらない確率がどうなるのか、具体的に求めてみましょう。
1回のくじを引いて、当たる確率が $\dfrac{1}{100}$ とします。このとき、当たらない確率は、 $\dfrac{99}{100}$ です。2回目でも3回目でも、100回目であっても、当たらない確率は同じ $\dfrac{99}{100}$ なので、100回引いても当たらない確率は\[ \left(\frac{99}{100}\right)^{100} \]となります。この値を、計算機を使って計算すると、だいたい $0.366\cdots$ となります。つまり、3人がこのガチャをそれぞれ100回引いた場合、一度も当たらない人が1人いる、という割合です。
では、何回引けば確率は、当たらない確率は 0 になるのでしょう。グラフをかいてみると次のようになります。 $y=0.99^x$ のグラフで、 $x$ がくじを引く回数、 $y$ が1度も当たらない確率を表しています。

300回引いても一度も当たらない確率は、約 4.9% です。20人いたら、残念な人が1人いる割合です。500回引いた場合は、約 0.66% です。この辺りまで来ると、結構 0 に近いと言えるかもしれません(グラフも x 軸にだいぶ近づいてます)が、それにしても、だいぶ引かないといけないですね。
これを上下反転させたもの( $y=1-0.99^x$ )は、 $x$ 回引いたときに、一度は当たる確率 $y$ を表します。

こうして見ると、途中から、引く回数を増やしていっても、「一度は当たる確率」はあまり増えていかないことがわかります(それまでに一度は当たっているから、と考えることもできますが)。
一回も当たらない確率はどこにいくか
ここまでは、当たる確率が1%のときに、くじを引く回数と「一度も当たらない確率」との関係を見てきました。100回引いても、必ず当たるとは限らないし、それどころか、一度も当たらない確率は37%近くもありました。
以下では、当たる確率が $\dfrac{1}{n}$ のときに、くじを $n$ 回引く場合を考えましょう(n は自然数)。n を大きくしていくと、一度も当たらない確率はどうなっていくでしょうか。
当たる確率が $\dfrac{1}{n}$ なら、当たらない確率は $1-\dfrac{1}{n}$ です。よって、 $n$ 回引いても一度も当たらない確率は\[ \left(1-\frac{1}{n}\right)^n \]となります。この式で、 $n$ をどんどん大きくしていくと、どうなるでしょうか。
カッコの中は $1$ に近づいていくので、全体も $1$ に近づいていく? それとも、 $1$ より小さいものをたくさん掛けるから、全体は $0$ に近づいていく?
これらの予想は、次のグラフを見れば、どちらも間違いだとわかります。
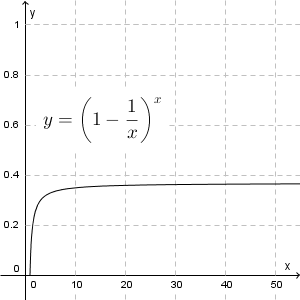
なんだか、40%弱のところで止まるような気がしますね。
このような「1に近いものをたくさん掛ける」極限は不定形の1つですが、今の場合は自然対数に帰着させることができます。式の形を見て気づいた人もいるかもしれませんが、【標準】自然対数と極限値の最後で見た次の式(一部文字を変えています)\[ e=\lim_{k\to\infty} \left(1+\frac{1}{k}\right)^k \]と似ていることがわかります。 $e$ の定義に帰着させるようにして、極限を求めてみましょう。定義に持っていきやすくするために、 $h=-\dfrac{1}{n}$ とおきます。
\begin{eqnarray}
& &
\lim_{n\to \infty} \left(1-\frac{1}{n}\right)^n \\[5pt]
&=&
\lim_{h\to -0} \left\{(1+h)^{\frac{1}{h} }\right\}^{-1} \\[5pt]
&=&
e^{-1}=\frac{1}{e} \\[5pt]
\end{eqnarray}となります。2行目から3行目で、波かっこの部分に対して、$e$ の定義を使った式変形を行っています。
$\dfrac{1}{e}$ は、だいたい $0.367879\cdots$ という値になります。上で見たグラフでも、これくらいの値のところに近づいているように見えます。
おわりに
ここでは、くじが当たらない確率を考えると、自然対数が出てくる、という話を見てきました。「1%のガチャを100回引いたら必ず当たる、もしくは、結構な確率で当たる」と考えるのは間違いです。37%程度の確率で、1度も当たらないことがあるのでした。この数字は $\dfrac{1}{e}$ に近い数字になることも見ました。全然関係がなさそうな場面で、自然対数が出てくるのはおもしろいですね。





