【基本】陰関数の微分（円の方程式と微分）

🕒 2018/09/21 🔄 2023/05/01

ここでは、円の方程式の微分を通じて、陰関数の微分について見ていきます。

📘 目次

円の方程式と微分

今まで、三次関数の微分や無理関数の微分、三角関数の微分や指数関数の微分などを見てきましたが、どれも $y=f(x)$ 型の関数の微分でした。しかし、中には、「 $y=$ 」の形で書けないものもあります。例えば、次のような円の方程式\[ x^2+y^2=1 \]です。 $x$ を決めても $y$ がいつもただ1つに決まるとは限りません。そのため、 $y$ は $x$ の関数とはいえません。しかし、 $x$ の変化に応じて $y$ がどのように変化するかは、場合分けをすれば調べることができます。

まず、 $y\geqq 0$ の場合を考えましょう。この場合、先ほどの円の方程式は\[ y=\sqrt{1-x^2} \]と変形することができます。こうなれば、無理関数の微分を計算するだけです。 $u=1-x^2$, $y=\sqrt{u}$ という合成関数の微分だと思えば、
\begin{eqnarray} \dfrac{dy}{dx} &=& \dfrac{dy}{du}\cdot\dfrac{du}{dx} \\[5pt] &=& \dfrac{1}{2} u^{-\frac{1}{2} }\cdot (-2x) \\[5pt] &=& \frac{1}{2\sqrt{1-x^2} }\cdot(-2x) \\[5pt] &=& -\frac{x}{\sqrt{1-x^2} } \\[5pt] \end{eqnarray}と計算できます。ここで、分母は $y$ と等しいので、微分した結果は $-\dfrac{x}{y}$ と書くことができます。なお、 $y=0$ のときは、微分することができません。

一方、 $y\lt 0$ のときも同じように計算すると、 $-\dfrac{x}{y}$ となることがわかります。つまり、 $y$ の符号によらずに\[ \dfrac{dy}{dx}=-\frac{x}{y} \]になる、ということですね。

実は、ここまでの計算はもっとシンプルに行うことができます。場合分けをしなくてもよくなります。

その方法は、円の方程式\[ x^2+y^2=1 \]の両辺を $x$ で微分する、という方法です。これにより、右辺は $0$ です。左辺の $x^2$ は $x$ で微分すると $2x$ ですね。残っている $y^2$ の部分ですが、これは、合成関数の微分だと思うと、\[ 2y\cdot\dfrac{dy}{dx} \]と書くことができます。

以上から、円の方程式の両辺を $x$ で微分すると
\begin{eqnarray} 2x+2y\cdot\dfrac{dy}{dx} &=& 0 \\[5pt] y\dfrac{dy}{dx} &=& -x \\[5pt] \end{eqnarray}となり、 $y\ne 0$ のときは\[ \dfrac{dy}{dx}=-\dfrac{x}{y} \]となることがわかります。

一般に、 $y=f(x)$ の形で書ける関数を、陽関数といいます。一方、 $x,y$ の関係が、 $x,y$ を用いた関数 $F(x,y)$ を使って $F(x,y)=0$ と書けているとき、陰関数といいます。

陰関数は、陽関数で表せるとは限りません。実際、円の方程式の場合は、1つの陽関数で表すことはできません。場合分けが必要でした。

$F(x,y)=0$ という陰関数で表示されている場合、 $\dfrac{dy}{dx}$ を求めるには、先ほどの円のときのように、両辺を $x$ で微分して解くことができます。

ちょっとあいまいな説明ですね。そもそも、「 $y$ が $x$ で微分できるかどうか」がわからないのに、合成関数の微分を使っているわけですからね。ただ、高校の範囲では、この細かいところには足を踏み入れず、「陰関数の両辺を微分する」ことができるものだとして考えることが一般的です。

円の方程式と微分を図形的に考える

最後に、円の方程式 $x^2+y^2=1$ を微分して得られた、\[ \dfrac{dy}{dx}=-\frac{x}{y} \]が、図形的にどのような意味を持っているかを見ておくことにしましょう。

$a,b\gt 0$ とし、 $a^2+b^2=1$ とします。ここで、点 $(a,b)$ での円の接線を考えてみましょう。この接線の傾きが、微分係数となる（参考：【基本】微分係数と導関数（の復習））わけなので、先ほどの計算では、傾きが $-\dfrac{a}{b}$ となることを求めたわけですね。

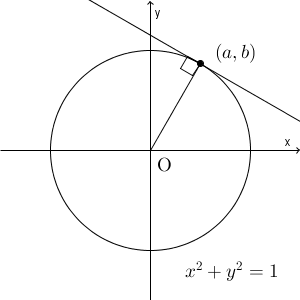
図形的に言えば、円の接線は、「円の中心と接点」を結んだ線と垂直に交わります。この直線は、原点と $(a,b)$ とを結んだ直線なので、傾きは $\dfrac{b}{a}$ ですね。接線はこの直線と垂直に交わりますが、2つの直線が垂直に交わることと、傾きの積が $-1$ になることは同値でした（参考：【基本】垂直な直線の方程式）。このことからも、接線の傾きが $-\dfrac{a}{b}$ となることがわかります。

つまり、円の方程式を微分して得られた式は、半径と垂直に交わる直線の傾きを求めたことと対応していた、というわけなんですね。