【応用】2倍角の公式を図形的に考えてみる

🕒 2018/05/28 🔄 2023/05/01

ここでは、円周角の定理を用いて、2倍角の公式を図形的に考えてみることにします。ここの内容は、正式な証明ではなく、知らなくても問題ないのですが、理解を深めるために見ていきます。

📘 目次

sinの2倍角の公式と三角形の面積

$\sin$ の2倍角の公式\[ \sin 2\theta=2\sin\theta \cos\theta \]を図形的に導く方法を見てみます。ひし形の面積を考える方法もあります（参考：【発展】ひし形の面積とsin2θ）が、ここでは、三角形の面積を考えます。

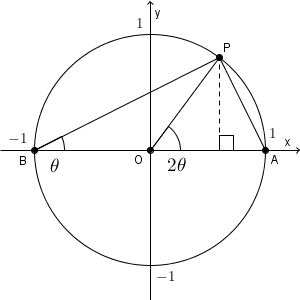
上の図のように、原点を $\mathrm{O}(0,0)$ とし、 $\mathrm{A}(1,0)$, $\mathrm{B}(-1,0)$ とします。また、原点を中心に点 A を反時計回りに $2\theta$ だけ回転して移動する点を P とおきます。ただし、 $0\lt 2\theta \lt \dfrac{1}{2}\pi$ とします（ただ、他の場合も、長さの符号などを変えれば、以下と同様の議論ができます）。

このとき、三角形 ABP の面積は
\begin{eqnarray} & & \dfrac{\mathrm{ AB }\cdot \mathrm{ OP }\sin \angle \mathrm{ POA } }{2} \\[5pt] &=& \dfrac{2\cdot 1 \cdot \sin 2\theta}{2} \\[5pt] &=& \sin2\theta \end{eqnarray}となります。

次に、線分 PB の中点を M としましょう。

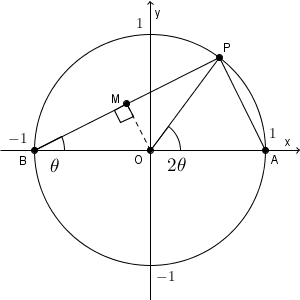
円周角の定理から $\angle \mathrm{ ABP }=\theta$ であり、 $\angle \mathrm{APB}=90^{\circ}$ だから、直角三角形 ABP の各辺の長さは、 $\mathrm{ AB }=2$, $\mathrm{ AP }=2\sin\theta$, $\mathrm{ BP }=2\cos\theta$ となります。よって、直角三角形 ABP の面積は\[ \frac{\mathrm{ AP }\cdot \mathrm{ BP } }{2}=2\sin\theta\cos\theta \]となります。

三角形 ABP の面積を2通りで出しましたが、これらは同じ値なので、\[ \sin 2\theta=2\sin\theta \cos\theta \]が成り立つことがわかります。2倍角の公式ですね。

cosの2倍角の公式も導いてみよう

上の図を用いて、 $\cos$ の2倍角の公式
\begin{eqnarray} \cos 2\theta &=& 2\cos^2\theta -1 \\[5pt] &=& 1-2\sin^2\theta \\[5pt] \end{eqnarray}を導くこともできます。

上の図で、点 P から線分 AB に垂線を下ろし、その足を H とします。

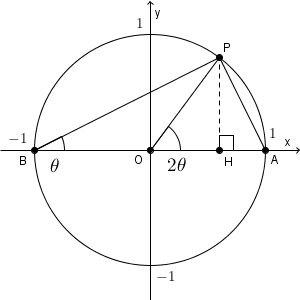
このとき、 $\cos 2\theta$ とは、線分 OH の長さのことですね。

直角三角形 ABP で考えると、 $\mathrm{ BP }=2\cos\theta$ となります。また、直角三角形 BPH で考えると、 $\mathrm{ BH }=2\cos^2 \theta$ となります。よって、
\begin{eqnarray} \mathrm{ OH } &=& \mathrm{ BH }-\mathrm{ BO } \\[5pt] &=& 2\cos^2\theta-1 \end{eqnarray}となります。よって、\[ \cos 2\theta = 2\cos^2\theta-1 \]が示せました。

また、直角三角形 ABP で考えると、 $\mathrm{ AP }=2\sin\theta$ となり、直角三角形 APH で考えると、 $\angle \mathrm{ APH }=\theta$ だから、 $\mathrm{ AH }=2\sin^2\theta$ となります。よって、
\begin{eqnarray} \mathrm{ OH } &=& \mathrm{ OA }-\mathrm{ AH } \\[5pt] &=& 1-2\sin^2\theta \\[5pt] \end{eqnarray}となり、\[ \cos 2\theta = 1-2\sin^2\theta \]を導くことができます。こうして2倍角の公式が導けます。