【基本】図で理解する正弦・余弦の加法定理
ここでは、正弦・余弦の加法定理を理解する図を見ていきます。正式な証明ではないですが、この図をかいて考えれば、加法定理を忘れてしまったとしても思い出せると思います。
三角関数の加法定理について
三角関数の加法定理とは、2つの角の和や差に対する三角関数の値についての定理です。具体的に書くと、次のような内容です。ここでは、和のみ紹介します。
\begin{eqnarray} \sin(\alpha+\beta) &=& \sin\alpha\cos\beta+\cos\alpha\sin\beta \\ \cos(\alpha+\beta) &=& \cos\alpha\cos\beta-\sin\alpha\sin\beta \\ \end{eqnarray}
見た目がごつい定理ですね。この証明や定理の使い方は別の箇所で見ますが、以下では、ある図を使って、この加法定理が示している内容を見ていきます。
2つの直角三角形を並べた図
先ほど見た加法定理の式について、どのような内容なのかを次の図を見て考えていきましょう。

2つの直角三角形を並べた図です。三角形 ABC は、 $\angle \mathrm{ C }$ が直角、 $\angle \mathrm{ ABC }=\alpha$ で、 $\mathrm{ AB }=1$ の直角三角形です。
この三角形の BC を斜辺とした直角三角形 BCD がその下にあります。 $\angle \mathrm{ D }$ が直角で、 $\angle \mathrm{ CBD }=\beta$ です。
さて、先ほど見た加法定理は、 $\alpha+\beta$ の三角関数の値に関するものでした。なので、 A から BD に垂線を下ろし、その足を E とおくことにしましょう。

こうすると\[ \sin(\alpha+\beta)=\mathrm{ AE },\ \cos(\alpha+\beta)=\mathrm{BE} \]であることがわかります。加法定理の左側が出てきましたね。なので、この式の右辺が、加法定理の右辺と対応していると予想できます。図を使って考えていきましょう。
この図に、さらに補助線をひきます。A から直線 CD にも垂線を引き、その足を F とおきましょう。

こうすると、三角形 ACF は直角三角形です。しかも、 $\angle \mathrm{ ACF }$ も $\angle \mathrm{ CBD }$ も $\angle \mathrm{ BCD }$ を足せば直角になることから、この2つの角は同じ大きさであることがわかります。つまり、\[ \angle \mathrm{ ACF }=\beta \]となります。
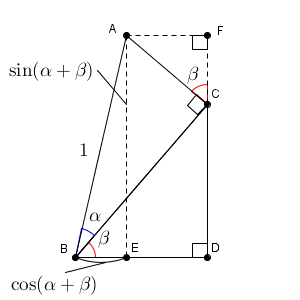
これらのことをふまえて、辺の長さを考えていきましょう。まず、直角三角形 ABC について考えれば\[ \mathrm{ AC }=\sin\alpha,\ \mathrm{ BC }=\cos\alpha \]となることがわかります。
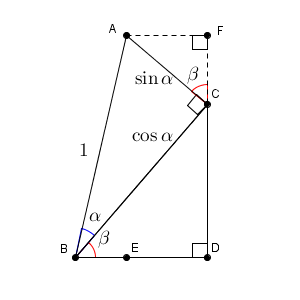
次に、直角三角形 ACF について考えると、例えば CF は
\begin{eqnarray}
\mathrm{ CF }
&=&
\mathrm{ AC }\cos\angle\mathrm{ ACF } \\[5pt]
&=&
\sin\alpha\cos\beta \\[5pt]
\end{eqnarray}となります。加法定理の右側に出てくる項の一部が出てきましたね。同じように考えれば\[ \mathrm{AF}=\sin\alpha\sin\beta \]となります。また、直角三角形 BCD についても同様に計算して\[
\mathrm{ CD }=\cos\alpha\sin\beta, \ \mathrm{ BD }=\cos\alpha\cos\beta \]となります。
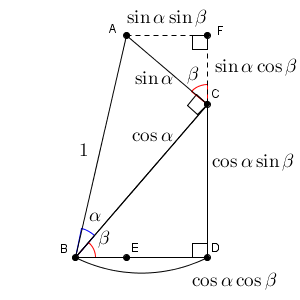
よって、下の図の通り、 $\mathrm{ AE }=\mathrm{ CF }+\mathrm{ CD }$ なので\[ \sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \]が成り立ちます。
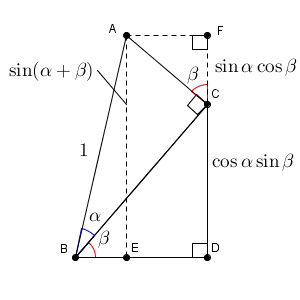
また、次の図から、 $\mathrm{ BE }=\mathrm{ BD }-\mathrm{ AF }$ なので\[ \cos(\alpha+\beta) = \cos\alpha\cos\beta-\sin\alpha\sin\beta \]が成り立ちます。

これらは、加法定理で出てきた式そのものです。
つまり、加法定理の内容は、直角三角形を2つ並べた図で考えれば、線分の長さを2通りに表しているだけ、と見ることができるわけですね。
おわりに
ここでは、正弦・余弦の加法定理を図で理解してみました。
以降のページで、加法定理について詳しく見ていきますが、もし公式を忘れてしまった場合は、ここでかいた図を用いて思い出してもいいでしょう。ただ、この図では、 $\alpha+\beta$ が鋭角の場合しか示せていないため、加法定理の証明できているわけではありません。その点は注意しましょう。





