【基本】媒介変数表示と微分
ここでは、円を通じて、媒介変数表示された関数の微分について見ていきます。
円の媒介変数表示と微分
【基本】陰関数の微分(円の方程式と微分)では、円の方程式 $x^2+y^2=1$ から、 $\dfrac{dy}{dx}=-\dfrac{x}{y}$ と計算できることを見ました。ここでは、円の方程式を媒介変数表示したときに、同じ結果が得られることを見ていきます。
媒介変数表示とは、 $x,y$ を、それぞれ別の文字の関数で表す方法のことを言います(参考:【基本】媒介変数表示)。媒介変数を使って表す方法はたくさんありますが、円の場合によく使われるものは\[ x=\cos t,\ y=\sin t \]と置く方法です。図形的には、原点を中心にして、点 $(1,0)$ を反時計回りに $t$ だけ回転した点を表しています。 $t$ を動かすことで、円全体が表現できます。
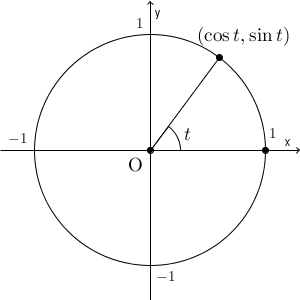
ここで、 $\dfrac{dy}{dx}$ を考えてみましょう。定義通りに計算するなら、 $x$ の変化量で $y$ の変化量を割り、 $x$ の変化量を $0$ に近づける、という計算をします。これを、媒介変数を使って、ぜんぶ $t$ で置き換えて考えてみます。そうすると、\[ \lim_{h\to 0} \dfrac{\sin(t+h)-\sin t}{\cos(t+h)-\cos t} \]を計算すればいいことがわかります。分母が $x$ の変化量、分子が $y$ の変化量で、分母分子の $x,y$ は対応しています。また、 $h\to 0$ のときに、分母は $0$ に収束するため、これは微分の定義の式を $t$ で置き換えたものになっています。
このままでは計算しづらいですが、分母分子を $h$ で割ってみると、 $\sin$ と $\cos$ の微分が使え、次のように計算できるようになります。
\begin{eqnarray}
& &
\lim_{h\to 0} \dfrac{\sin(t+h)-\sin t}{\cos(t+h)-\cos t} \\[5pt]
&=&
\lim_{h\to 0} \dfrac{\frac{\sin(t+h)-\sin t}{h} }{\frac{\cos(t+h)-\cos t}{h} } \\[5pt]
&=&
\dfrac{(\sin t)'}{(\cos t)'} \\[5pt]
&=&
-\dfrac{\cos t}{\sin t} \\[5pt]
\end{eqnarray}$x=\cos t$, $y=\sin t$ だったのだから、この結果は $-\dfrac{x}{y}$ であり、冒頭で振り返った結果と同じになりましたね。
ここまでの計算を、図形的に考えてみましょう。円上の点 $(\cos t,\sin t)$ に対して、この点と原点とを結んだ直線の傾きは $\tan t$ です。よって、この点での接線の傾きは $-\dfrac{1}{\tan t}$ です。垂直に交わる2つの直線は、傾きの積が $-1$ になるからです。
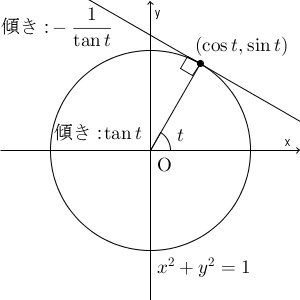
接線の傾きが微分した結果に対応しますが、先ほどの微分した結果は\[ -\dfrac{\cos t}{\sin t}=-\frac{1}{\tan t} \]と書けることから、図形的に考えた結果と微分の計算結果があっていることがわかります。
媒介変数表示と微分
先ほどは、円の媒介変数表示をもとに、微分の計算を行いました。その途中で、「 $y$ を $t$ で微分したものを、 $x$ を $t$ で微分したもので割る」という式が出てきました。これが媒介変数表示された関数の微分でのキーとなります。以下では、一般的な状況で書き直してみます。
$x=f(t)$, $y=g(t)$ というように、媒介変数表示されていたとします。また、 $f(t)$, $g(t)$ は、ともに微分可能であるとします。ここで、 $\dfrac{dy}{dx}$ を考えてみます。そのためには、次の極限を計算すればいいです。\[ \lim_{h\to 0} \dfrac{g(t+h)-g(t)}{f(t+h)-f(t)} \]分母が $x$ の変化量、分子が $y$ の変化量を表しています。 $t$ のときと $t+h$ のときの変化量を表しているので、分母分子での $x,y$ の対応もあっています。また、 $h\to 0$ としたときに分母は $0$ に収束するので、これを計算すると $\dfrac{dy}{dx}$ が得られます。先ほどと同様に、分母・分子を $t$ で割ると
\begin{eqnarray}
& &
\lim_{h\to 0} \dfrac{g(t+h)-g(t)}{f(t+h)-f(t)} \\[5pt]
&=&
\lim_{h\to 0} \dfrac{\frac{g(t+h)-g(t)}{h} }{\frac{f(t+h)-f(t)}{h} } \\[5pt]
&=&
\dfrac{\dfrac{dy}{dt} }{\dfrac{dx}{dt} } \\[5pt]
\end{eqnarray}となります。これが、微分した結果となります。
おわりに
ここでは、媒介変数表示された関数の微分について見てきました。それぞれを微分したものを割ることで、微分が計算できるのでした。媒介変数表示された関数は、 $y=f(x)$ の形に変形できないことが多いため、微分するときには必須のツールとなります。





