【標準】極値から係数を求める

🕒 2018/10/26 🔄 2023/05/01

ここでは、極値から係数を求める問題を考えます。間違いやすい点があるので、注意して見ていきましょう。

📘 目次

極値から係数を求める

例題

関数 $f(x)=(ax+1)e^x$ が $x=0$ で極値をとるとき、 $a$ の値を求めなさい。

$x=0$ で極値をとるのだから、【基本】極大値と極小値（の復習）で見たように、 $f'(0)=0$ となります。これを利用して $a$ の値を求めましょう。

まず、関数を微分して
\begin{eqnarray} f'(x) &=& ae^x+(ax+1)e^x \\[5pt] &=& \{a(x+1)+1\}e^x \\[5pt] \end{eqnarray}となるので、 $f'(0)=0$ とすると \begin{eqnarray} (a+1)e^0 &=& 0 \\[5pt] a &=& -1 \end{eqnarray}となります。よって、 $a=-1$ 、とやってしまいがちですが、ここで終わってはいけません。

【基本】極大値と極小値（の復習）でも見ましたが、「極値をとるなら、微分係数が0」ですが、逆は成り立ちません。 $f'(0)=0$ でも、 $x=0$ で極値をとるとは限りません。例えば、 $y=x^3$ は $x=0$ での微分係数は $0$ ですが、これは単調増加関数であり、 $x=0$ で極値はとりません。

上の計算では、「 $x=0$ で極値をとるなら $a=-1$ しかありえない」ということがわかっただけで、本当に「 $a=-1$ なら $x=0$ で極値をとるかどうか」はわかりません。なので、ちゃんと極値をとることを確認する必要があります。

確認する方法は、普通に極値を求めるときと同じです。増減表をかいて確かめます。

$a=-1$ とすると\[ f'(x)=-xe^x \]となるので、増減表は次のようになります。
\begin{array}{c|ccccccc} x & \cdots & 0 & \cdots \\ \hline y' & + & 0 & - \\ \hline y & \nearrow & & \searrow \end{array}よって、たしかに $x=0$ で極大となることがわかります。このことから、 $a=-1$ が答えとなります。

指数関数とn乗の発散速度

先ほど求めた関数 $f(x)=(-x+1)e^x$ のグラフはどうなるでしょうか。増減表までわかっているので簡単にかけそうですが、範囲の右端・左端は少し考えないといけません。

まず、右端、つまり、 $x\to\infty$ の場合は問題ないでしょう。 $x,e^x$ はともに正の無限大に発散するので、 $f(x)\to-\infty$ となります。問題は $x\to-\infty$ の場合です。

$t=-x$ とおいて、\[ \lim_{t\to\infty} \frac{t+1}{e^t} \]を考えてみましょう。分母も分子も両方正の無限大に発散するので、これは不定形です。なので、工夫して計算する必要があります。

ただ、これを計算するのは少し難しいので、結論だけを書きましょう。指数関数は、多項式関数よりも、発散速度が速い、ということを使います。これにより、\[ \lim_{t\to\infty}\frac{t}{e^t}=0 \]となります。よって、\[ \lim_{x\to-\infty} f(x)=0 \]となります。

指数関数が多項式関数よりも発散速度が速い、という話は、【応用】指数関数の発散速度で見ています。 $e^t\gt 2^t$ を使い、二項定理を利用することで示すことができます。

$x\to\infty$ や $x\to-\infty$ としたときに、 $x^n$, $e^x$, $\log x$ の積や商が含まれている場合、極限を考えるのは少し難しいです。問題を解く中でこれらの極限を求める必要がある場合は、問題文中に与えられていることもあります。例えば、「 $x\to\infty$ のとき $xe^{-x}\to 0$ となることは使ってもよい」みたいな感じですね。

ただ、いつも与えられているも限らないので、「指数関数、多項式関数、対数関数は、発散速度はこの順番に速い」ということは知っておいた方が役立つでしょう。

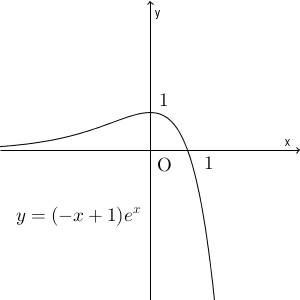
今までの内容をまとめると、 $y=(-x+1)e^x$ のグラフは次のようになります。