【応用】図形と微分と最大・最小

ここでは、微分を利用して最大・最小を考える問題のうち、図形が絡むものを見ていきます。

球に内接する直円柱

直円柱というのは、ざっくりいうと、まっすぐな円柱ということで、もう少し厳密にいうと、底面の中心同士を結んだ直線が底面に垂直な円柱ということです。図は次ようになっています。

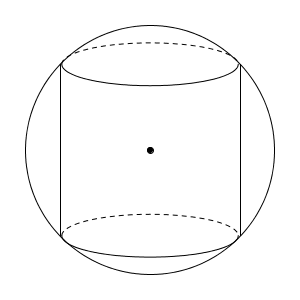
体積の最大を考えるためには、円柱の底面の半径と高さがわからないとダメですね。わからないものが2つありますが、球に内接していることを利用して、半径と高さの関係を見ることから始めましょう。

こうした立体の問題は、スパっと切って、平面にしたほうが考えやすくなります。

どの断面を考えるかは、場合によって異なりますが、球が絡む問題であれば、球の中心を含む面で切ることが多いです。また、「球に内接している」という条件が使えるように、球と円柱が接している部分も含んだほうがよさそうです。

つまり、円柱の底面に垂直な平面で切った断面を考えたほうがいい、ということです。このときの断面は、次のようになります。

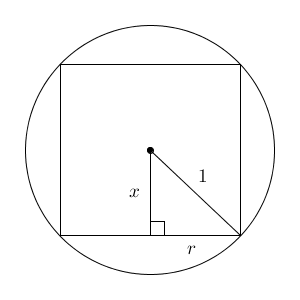
底面の半径を $r$ とし、高さの半分を $x$ としています。このとき、\[ x^2+r^2=1 \]が成り立ちます。これから、円柱の体積の最大値を考えたいわけですが、半径を大きくしようとすると高さが小さくなり、高さを大きくしようとすると半径が小さくなってしまう、ことがわかります。この例題では、半径も高さもほどよく大きくできるケースを探す、ということですね。

さて、 $x,r$ の関係式があるので、 $x$ を動かすか、 $r$ を動かすか、どちらをメインで動かすかを決めなければいけません。これは、あとでわかるように、 $x$ を動かして考えたほうが楽になります。高さの半分である $x$ を使って、体積を表してみましょう。

円柱の高さの半分を $x$ とすると、底面の半径 $r$ は $\sqrt{1-x^2}$ となります。このときの円柱の体積を $V$ とすると
\begin{eqnarray} V &=& \pi r^2 \times 2x \\[5pt] &=& 2\pi x(1-x^2) \\[5pt] \end{eqnarray}となります。これを微分して増減表をかけば、最大値が求められそうですね。

ちなみに、 $r$ の方を動かして考えようとしていたら、高さが $2\sqrt{1-r^2}$ と書けることから
\begin{eqnarray} V = 2\pi r^2\sqrt{1-r^2} \end{eqnarray}となります。根号が入っているので、これを微分するのはめんどくさそうです。上で見たように、 $x$ の式で書けば、根号はなく、扱いやすいことがわかります。

体積を考えるときに、「半径の2乗」が出てくるので、うまく根号が消えるんですね。高さの方を動かした方がいいことがわかるでしょう。

さて、 $V=2\pi x(1-x^2)$ ですが、 $2\pi$ は定数なので、他の部分の最大を考えればいいでしょう。\[ f(x)=x(1-x^2)=x-x^3 \]とおいて、これの最大値を考えましょう。
\begin{eqnarray} f'(x)=1-3x^2 \end{eqnarray}なので、 $f'(x)=0$ とすると $x=\pm\dfrac{\sqrt{3} }{3}$ となります。

これをもとに増減表をかきたいのですが、 $x$ はどういう範囲を動くでしょうか。まず、高さは正でないといけないので、 $x\gt 0$ です。 $x$ が $0$ に近づいていくと、円柱は平べったくなって、つぶれていきます。

また、半径 $1$ の球に内接していることから、 $1$ になることもありません。 $1$ に限りなく近づけることはできますが、 $1$ に近づけていくと、円柱は細長くなって、つぶれていきます。

よって、定義域は $0\lt x\lt 1$ となります。増減表は次のようになります。
\begin{array}{c|cccc} x & 0 & \cdots & \dfrac{\sqrt{3} }{3} & \cdots & 1 \\ \hline f'(x) & \times & + & 0 & - & \times \\ \hline f(x) & \times & \nearrow & & \searrow & \times \end{array}この増減表から、 $f(x)$ が最大となるのは $x=\dfrac{\sqrt{3} }{3}$ のときであることがわかります。このときに体積も最大になります。

よって、円柱の体積が最大になるとき、底面の半径は
\begin{eqnarray} \sqrt{1-\frac{1}{3} }=\dfrac{\sqrt{6} }{3} \end{eqnarray}であり、高さは\[ 2\times\dfrac{\sqrt{3} }{3}=\dfrac{2\sqrt{3} }{3} \]であり、体積は \begin{eqnarray} & & 2\pi \cdot \dfrac{\sqrt{3} }{3} \left(1-\dfrac{1}{3}\right) \\[5pt] &=& \dfrac{4\sqrt{3} }{9}\pi \\[5pt] \end{eqnarray}となることがわかります。

おわりに

ここでは、図形が絡んだ最大・最小を求める問題で、微分を使うものを見ました。何を変数として、どのような関数を考えるか、この選択を間違うと、計算量がかなり増えてしまいます。普段から、単純に問題を解くだけでなく、計算量を減らす解き方ができないか、考えるようにしましょう。それが時間の節約にもなりますし、計算間違いを減らすことにもつながります。