【基本】変曲点

ここでは、上に凸と下に凸の境目である変曲点について見ていきます。

変曲点

$\def\EtoN{\class{EtoN}{} }\def\EtoS{\class{EtoS}{} }\def\NtoE{\class{NtoE}{} }\def\StoE{\class{StoE}{} }$【基本】上に凸と下に凸で見たように、関数 $f(x)$ が、連続な第二次導関数 $f^{\prime\prime}(x)$ を持っているとき、 $f'(x)$ が減っていく区間、言い換えれば、 $f^{\prime\prime}(x)\lt 0$ の区間では上に凸といい、 $f'(x)$ が増えていく区間、つまり、 $f^{\prime\prime}(x)\gt 0$ の区間では下に凸というのでした。

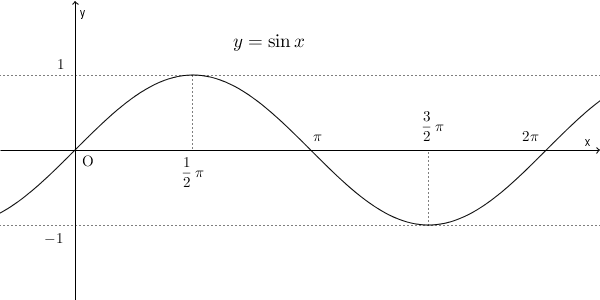
$f(x)=\sin x$ であれば、 $f^{\prime\prime}(x)=-\sin x$ なので、 $0\lt x\lt \pi$ の範囲では上に凸、 $\pi\lt x\lt 2\pi$ の範囲では下に凸、などとなります。

$0\leqq x\leqq 2\pi$ の範囲を見ると、 $x=\pi$ で、上に凸と下に凸が切り替わることがわかります。 $f'(x)$ のときも、符号が変わるところを極値と言いましたが、 $f^{\prime\prime}(x)$ に対しても、 $f^{\prime\prime}(x)$ の符号が変わるところには名前がついていて、変曲点(inflection point) といいます。 $f^{\prime\prime}(x)$ がプラスからマイナスに変わるところも、マイナスからプラスに変わるところも、どちらも変曲点と言います。

$f^{\prime\prime}(x)$ の符号が変わるところを変曲点と呼ぶため、 $(a,f(a))$ が変曲点ならば、 $f^{\prime\prime}(a)$ は $0$ となります。

ただ、逆は成り立ちません。 $f^{\prime\prime}(a)=0$ でも、変曲点とは限りません。 $f^{\prime\prime}(x)$ が、プラス→0→プラスとなったり、マイナス→0→マイナスとなる可能性があるからです。これは、 $f'(x)=0$ でも極値をとるとは限らない、ということに似ていますね。

上に凸・下に凸と増減表

さて、 $f'(x)$ だけでなく、 $f^{\prime\prime}(x)$ についても調べることで、 $f(x)$ の増減だけでなく、上に凸か下に凸かもわかるようになりました。

そのため、 $x$ が増加していったときの $y=f(x)$ の変化として、次の4パターンを見分けられるようになったことになります。

• $y$ は増え、増え方は速くなっていく $(y'\gt 0, y^{\prime\prime}\gt 0)$
• $y$ は増えるが、増え方は遅くなっていく $(y'\gt 0, y^{\prime\prime}\lt 0)$
• $y$ は減り、減り方は速くなっていく $(y'\lt 0, y^{\prime\prime}\lt 0)$
• $y$ は減るが、減り方は遅くなっていく $(y'\lt 0, y^{\prime\prime}\gt 0)$

増減表に2階微分まで書くかどうかは状況によりますが、もし書く場合は、上の4パターンを、それぞれ $\EtoN$, $\NtoE$, $\EtoS$, $\StoE$ と書きます。

$y=\sin x\ (0\leqq x\leqq 2\pi)$ の場合で書くと、 $y'=\cos x$, $y^{\prime\prime}=-\sin x$ なので、増減表は次のようになります。

\begin{array}{c|ccccccccc} x & 0 & \cdots & \dfrac{1}{2}\pi & \cdots & \pi & \cdots & \dfrac{3}{2}\pi & \cdots & 2\pi \\ \hline y' & + & + & 0 & - & - & - & 0 & + & + \\ \hline y^{\prime\prime} & 0 & - & - & - & 0 & + & + & + & 0 \\ \hline y & 0 & \NtoE & 1 & \EtoS & 0 & \StoE & -1 & \EtoN & 0 \end{array}

$x=\dfrac{1}{2}\pi$ で極大、 $x=\dfrac{3}{2}\pi$ で極小となり、点 $(\pi,0)$ が変曲点であることがわかります。

この増減表と、 $y=\sin x$ のグラフを見比べてみましょう。

たしかに、丸まっている矢印の通りの形になっていますね。

今は、すでに知っている関数 $y=\sin x$ のグラフから、微分とグラフの対応を見ていますが、今後は、初めて見る関数に対して、2階微分を計算して増減表をかき、増減や凹凸を把握したうえで、グラフの概形をかいていくことになります。

おわりに

ここでは、凹凸の切り替わる変曲点について見た後、2階微分も加えた増減表を見ました。2階微分まで調べることで、グラフに関する情報がかなりわかるようになります。