【基本】上に凸と下に凸

🕒 2018/10/20 🔄 2023/06/27

ここでは、接線の傾きの変化について見ていきます。

📘 目次

上に凸と下に凸

$f(x)=\sin x$ のグラフを考えてみましょう。 $f'(x)=\cos x$ なので、 $0\leqq x \leqq 2\pi$ での増減表をかくと、次のようになります。

\begin{array}{c|ccccccc} x & 0 & \cdots & \dfrac{1}{2}\pi & \cdots & \dfrac{3}{2}\pi & \cdots & 2\pi \\ \hline f'(x) & & + & 0 & - & 0 & + & \\ \hline f(x) & 0 & \nearrow & 1 & \searrow & -1 & \nearrow & 0 \end{array}

ただ、 $y=\sin x$ のグラフは、増減表をかかなくても、すでに知っていますね。次のようになります。（参考：【基本】三角関数のグラフ）

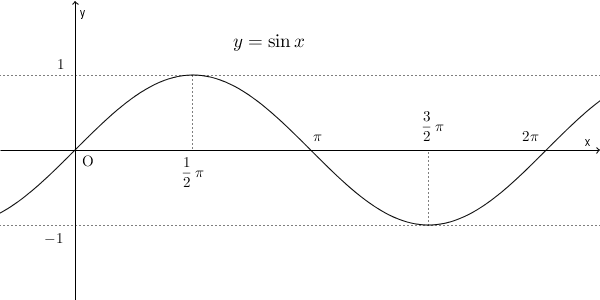
この $\dfrac{1}{2}\pi\leqq x\leqq\dfrac{3}{2}\pi$ のところを見てみると、 $f'(x)=0$ から始まって負の値をとり、また $0$ に戻っています。

このことから、この区間では、 $f'(x)$ は $0$ からしばらくの間は減っていき、途中から増えて $0$ に近づいていく、と予想できます。下の図は、各点での接線の動きを見たものですが、たしかにそうなっています。

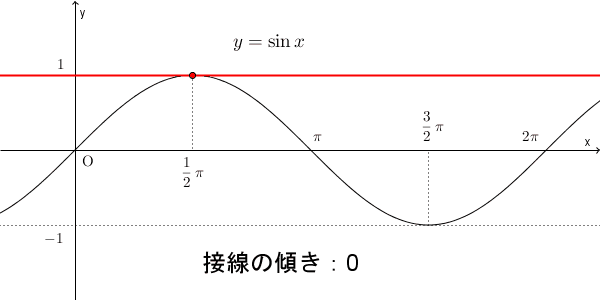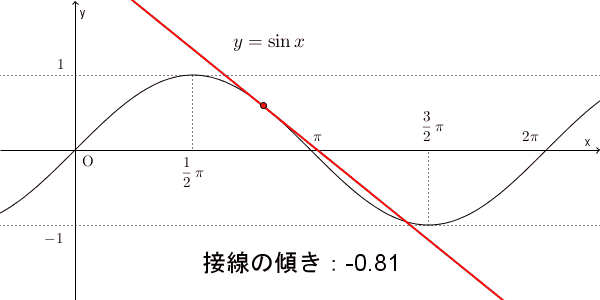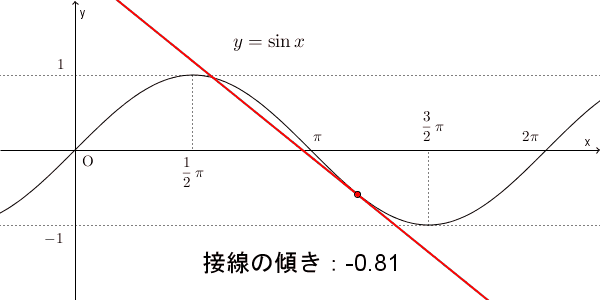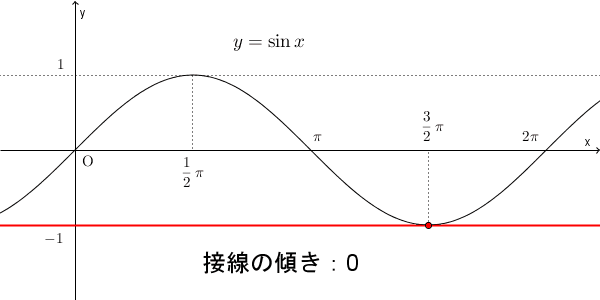
$f'(x)$ を調べることで、 $f(x)$ の増減がわかるのでしたね。 $f'(x)$ が正なら増える、負なら減るのでした。このように、今までは $f'(x)$ の符号に注目していましたが、 $f'(x)$ の値がどんどん減っていくと、どういうことが起こるか考えてみましょう。

これを考えるには、 $f'(x)$ が $f(x)$ の変化を表していることを利用しましょう。そうすると、 $f'(x)$ がどんどん減っていくということは、 $f(x)$ の増えるペースが遅くなる、もしくは、減るペースが速くなる、と考えられます。

このように、 $f'(x)$ がどんどん減って、グラフが上の方に膨らんでいる形になっているとき、この曲線は上に凸（とつ）(convex) であるといいます。

逆に、 $f'(x)$ がどんどん増えていくと、 $f(x)$ の減るペースが遅くなる、増えるペースが速くなる、と考えられます。

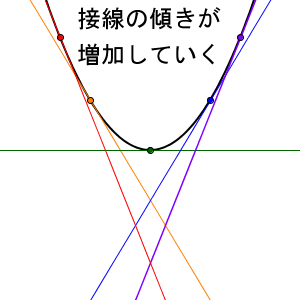
$f'(x)$ がどんどん増えて、グラフが下の方に膨らんでいるとき、この曲線は下に凸(concave) である、といいます。

グラフが上に凸か下に凸かを考えるには、 $f'(x)$ の増減を調べる必要があります。この調べ方は「 $f(x)$ の増減を調べるために $f'(x)$ の符号を調べた」ことから考えるとわかるでしょう。 $f'(x)$ の増減は、 $f^{\prime\prime}(x)$ の符号を調べるとわかります。

以上のことをまとめると、次のようになります。

上に凸と下に凸

関数 $f(x)$ は、連続な第2次導関数 $f^{\prime\prime}(x)$ を持つとする。このとき、以下が成り立つ。

ある区間で $f^{\prime\prime}(x)\lt 0$ ならば、その区間で $y=f(x)$ は上に凸である。
ある区間で $f^{\prime\prime}(x)\gt 0$ ならば、その区間で $y=f(x)$ は下に凸である。

$f(x)=\sin x$ の場合であれば、 $f'(x)=\cos x$, $f^{\prime\prime}(x)=-\sin x$ なので、 $0\lt x\lt \pi$ の区間では上に凸、 $\pi\lt x\lt 2\pi$ の区間では下に凸、となります。これを踏まえて、もう一度グラフを見てみましょう。

たしかに、グラフを見れば、上に凸、下に凸という名にふさわしい形のグラフになっています。