【標準】微分と三角関数のグラフ
ここでは、微分を用いて、三角関数を含んだ関数のグラフをかいていきます。
三角関数を含んだ関数のグラフ
今回は、 $x\to\infty$ の場合などを考えないし、 $y\to\infty$ などともならないので、漸近線はありません。
まずは、微分をして、増減について考えましょう。
\begin{eqnarray}
y'
&=&
1+2\sin x
\end{eqnarray}となります。 $y'=0$ とすると、 $\sin x=-\dfrac{1}{2}$ なので、今考えている範囲では、 $x=\dfrac{7}{6}\pi,\dfrac{11}{6}\pi$ となります。
次に、凹凸を考えるために、もう一度微分しましょう。
\begin{eqnarray}
y^{\prime\prime}
&=&
2\cos x
\end{eqnarray}となります。これから、上に凸となる範囲、下に凸となる範囲がわかります。
$\def\EtoN{\class{EtoN}{} }\def\EtoS{\class{EtoS}{} }\def\NtoE{\class{NtoE}{} }\def\StoE{\class{StoE}{} }$$\require{cancel}$これらを踏まえて、増減表をかくと、次のようになります。
\begin{array}{c|ccccccccc}
x & \frac{\pi}{2} & \cdots & \frac{7}{6}\pi & \cdots & \frac{3}{2}\pi & \cdots & \frac{11}{6}\pi & \cdots & 2\pi \\
\hline
y' & + & + & 0 & - & - & - & 0 & + & + \\
\hline
y^{\prime\prime} & 0 & - & - & - & 0 & + & + & + & + \\
\hline
y & & \NtoE & & \EtoS & & \StoE & & \EtoN &
\end{array}これより、 $x=\dfrac{7}{6}\pi$ のときに極大値 $y=\dfrac{7}{6}\pi+\sqrt{3}$ をとり、 $x=\dfrac{11}{6}\pi$ のときに極小値 $y=\dfrac{11}{6}\pi-\sqrt{3}$ をとることがわかります。また、グラフは、次のようになります。
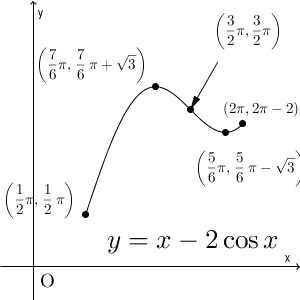
なお、 $\left(\dfrac{3}{2}\pi,\dfrac{3}{2}\pi\right)$ は、変曲点になります。
最大値と最小値
先ほどの例題では、関数のグラフをかきました。グラフをかくために、極値を求めましたね。このグラフをよく見ると、最大値と最小値もわかります。
最大値は、 $x=\dfrac{7}{6}\pi$ のときにとることがわかります。これは、極大値と一致します。一方、最小値は、 $x=\dfrac{1}{2}\pi$ のときであり、極小値と一致しているわけではありません。
一般に、最大値と極大値、最小値と極小値は一致しません。極大値とは、「その付近で一番大きな値」というだけであり、考えている範囲全体で一番大きな値とは限りません。
この話は、すでに過去に出てきています。【基本】微分と最大値・最小値も、必要ならば見直しておきましょう。
おわりに
ここでは、三角関数を含んだ関数のグラフをかきました。また、範囲が限定されていたので、最大値・最小値の話も見ました。これらと、極大値・極小値との違いについて、混同しないようにしましょう。





