【標準】微分可能でない関数と極値
ここでは、微分可能でない点を含む関数に対して極値を求める問題を見ていきます。絶対値を含む関数を考えていきます。
微分可能でない関数の極値
【基本】微分可能性と連続性で見たように、絶対値を含む関数は微分できないことがあります。この例題でも、あとで計算してわかるように、微分できない箇所があります。ただ、微分できない箇所は一部分なので、その点だけに注意して考えていきましょう。
まず、 $\sqrt{x+2}$ が含まれていることから、定義域は $x\geqq -2$ であることがわかります。この範囲で考えていきましょう。
絶対値の部分 $|x-1|$ がそのまま残っていると、微分することができません。場合分けをして、絶対値を外して考えていきます。
$x\geqq 1$ の場合は、\[ f(x)=(x-1)\sqrt{x+2} \]となります。これは微分可能な関数なので、 $x\geqq 1$ の範囲で微分すると
\begin{eqnarray}
f'(x)
&=&
1\cdot\sqrt{x+2}+(x-1)\frac{1}{2\sqrt{x+2} } \\[5pt]
&=&
\frac{2(x+2)+(x-1)}{2\sqrt{x+2} } \\[5pt]
&=&
\frac{3(x+1)}{2\sqrt{x+2} } \\[5pt]
\end{eqnarray}となります。 $x\geqq 1$ の範囲では、 $f'(x)\gt 0$ なので、この範囲では単調増加であることがわかります。
次に、 $-2 \leqq x\lt 1$ について考えましょう。このときは\[ f(x)=(1-x)\sqrt{x+2} \]となります。先ほどの結果を $-1$ 倍したものなので、この範囲で微分すると\[ f'(x)=-\frac{3(x+1)}{2\sqrt{x+2} } \]となります。 $f'(x)=0$ とすると $x=-1$ となります。
$x=1$ では、微分係数を定めることはできません。上で見た計算からもわかる通り、左側極限・右側極限はそれぞれ存在しますが、 $-\sqrt{3}$ と $\sqrt{3}$ なので、符号が異なります。つまり、一致しません。なので、 $x=1$ で接線をひくことができません。
ただ、今の場合は、 $x=1$ で連続であることがわかればそれで大丈夫です。増減表は、 $x=1$ のところを無視して、次のようにして書くことができます。
\begin{array}{c|cccc}
x & -2 & \cdots & -1 & \cdots & 1 & \cdots \\
\hline
f'(x) & \times & + & 0 & - & \times & + \\
\hline
f(x) & 0 & \nearrow & & \searrow & 0 & \nearrow
\end{array}この増減表から、 $x=1$ のときに極小値 $0$ をとることがわかります。また、極大となるのは $x=-1$ のときで、その値は
\begin{eqnarray}
f(-1)
&=&
2
\end{eqnarray}となります。
ちなみに、グラフは次のようになります。
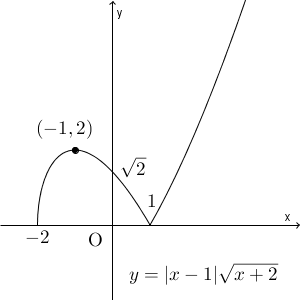
$x=1$ のところのように、とがっている部分では接線がひけないし、微分係数を定義することもできません。
微分可能であれば、「 $f'(x)=0$ となるところが極値をとる候補」と考えることができます。しかし、微分可能でない点はこの考え方は使えません。しかも、上の例題のように、その微分可能でない点で極値をとることもあります。
そのため、微分可能でない部分のある関数は、その前後での $f'(x)$ の符号を調べることになります。結局、増減表をかくことになるので、やることは今までと変わりませんが。
おわりに
ここでは、微分できない点を含む関数の極値を求める問題を考えました。微分できない点に注意しながら、増減表をかいて考えましょう。





