【応用】方程式の実数解の個数と微分
ここでは、方程式の実数解の個数を調べるために、微分を応用する問題を見ていきます。
方程式の実数解の個数
方程式の異なる実数解の個数ということは、 $y=e^x$ と $y=ax^2$ のグラフの共有点の個数だと言い換えることができます。似たような考え方は、【標準】三次方程式の実数解の個数でも使っています。
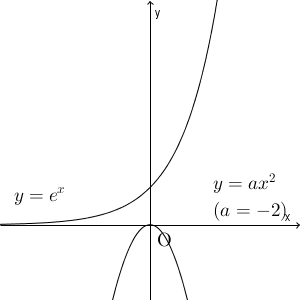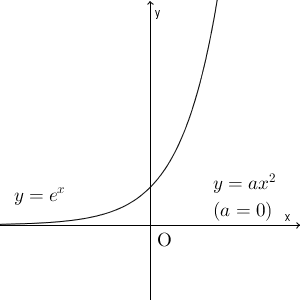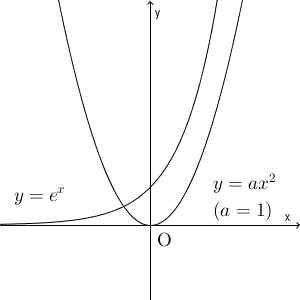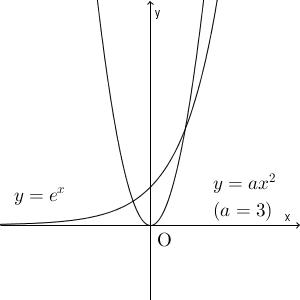
$a=0$ のときは $y=ax^2$ は $x$ 軸と一致し、 $a\lt 0$ のときは、グラフは $y\leqq 0$ の範囲に含まれるため、これらのときは、 $y=e^x$ と共有点は持たないので、実数解の個数は $0$ です。
$a\gt 0$ のときは、 $x\lt 0$ のところで、共有点を持つことがわかります。また、 $a$ が大きくなると、放物線は徐々に鋭くなっていくため、 $x\gt 0$ の部分でも共有点を持つようになります。こうしたことから、たしかに $a$ の値によって共有点の個数は変わると考えられます。
この考え方では、動いているものが2つあると考えています。 $a$ を動かすことで放物線がどうなるかを考え、次にそのときの $x$ について考える、という流れですね。ただ、2つのものが動くと面倒ですし、そもそも $a$ によって状況が変わるので、考えないといけない場合分けの種類が増えてしまいます。
そこで、両辺にある $a,x$ を片方ずつに分けて、それぞれの文字に集中できるようにして考えることにしましょう。
$x=0$ が解になることはありません。なので、 $x\ne 0$ の場合を考えます。元の方程式の両辺を $x^2$ で割って\[ \dfrac{e^x}{x^2}=a \]について考えることにしましょう。こうすると、左辺は $x$ だけの式なので、左辺の関数の取りうる値を調べれば、実数解の個数が調べやすくなります。
$f(x)=\dfrac{e^x}{x^2}$ $(x\ne 0)$ とおいて、これを微分すると
\begin{eqnarray}
f'(x)
&=&
\frac{e^x x^2-2x e^x}{x^4} \\[5pt]
&=&
\frac{e^x (x-2)}{x^3} \\[5pt]
\end{eqnarray}となります。よって、増減表は次のようになります。
\begin{array}{c|cccc}
x & \cdots & 0 & \cdots & 2 & \cdots \\
\hline
f'(x) & + & / & - & 0 & + \\
\hline
f(x) & \nearrow & / & \searrow & & \nearrow
\end{array}極小値は\[ f(2)=\dfrac{e^2}{4} \]です。また、 $x\to -\infty$ としたとき、 $f(x)\to 0$ となります。 $x\to 0$ のときは、 $f(x)\to\infty$ となります。 $x\to\infty$ のときは、【応用】微分を用いた不等式の証明で見たように、 $f(x)\to\infty$ となります。
増減表とこれらの極限から、 $f(x)=\dfrac{e^x}{x^2}$ のグラフは次のようになります。

これと直線 $y=a$ との共有点を考えましょう。 $y=a$ は、 $a$ の大きさによって上下するだけなので、共有点の数も数えやすいです。
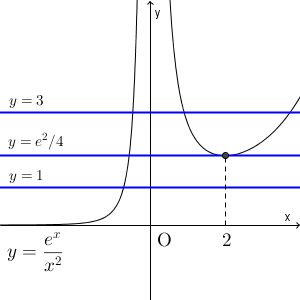
上の青線は、 $y=1,\dfrac{e^2}{4},3$ のときをそれぞれ表しています。このグラフから共有点の数、つまり、もとの方程式の実数解の個数がわかります。
グラフから、
- $a\gt\dfrac{e^2}{4}$ のときは3個
- $a=\dfrac{e^2}{4}$ のときは2個
- $0\lt a \lt \dfrac{e^2}{4}$ のときは1個
- $a\leqq 0$ のときは0個
というのが答えとなります。
もし、文字を分けずに、 $g(x)=e^x-ax^2$ のグラフをかいていたらどうなっていたでしょうか。このグラフと $x$ 軸との共有点を考えることもできますが、\[ g'(x)=e^x-2ax \]となります。もうこの時点でやっかいな感じがしますね。増減表をかくには、 $g'(x)=0$ となる場合を考えるわけですが、きれいに求められないですね。さらに、 $y=g(x)$ の極値の正負も考えないといけません。なかなかハードルが高そうです。
2つの文字の式に分解できる場合は、分解して考えたほうがいいでしょう。
おわりに
ここでは、方程式の実数解の個数を考えるために、微分を用いる方法を見ました。方程式の左辺から右辺を引いたものを関数と考えて、そのまま微分できる場合もありますが、上で見たように2つの文字の式に分解してから考えたほうがいい場合もあります。





