【標準】微分と関数のグラフと漸近線

🕒 2018/10/23 🔄 2023/05/01

ここでは、関数のグラフをかくときに必要となる、漸近線について見ていきます。

📘 目次

定義域の境目や端っこについて

例題

次の関数の増減、極値、凹凸、漸近線を調べて、グラフをかきなさい。\[ y=x+\dfrac{1}{x} \]

曲線がある直線に限りなく近づいていくとき、その直線のことを漸近線(asymptote) と言います。漸近線は、【基本】双曲線と漸近線や【基本】一次分数関数のグラフなどでも出てきていますが、このページの後半で、もう少し詳しく見ることにしましょう。

【基本】微分と関数のグラフを参考にしつつ考えていきましょう。まず、増減を調べるために微分をして
\begin{eqnarray} y' &=& 1-\frac{1}{x^2} \\[5pt] \end{eqnarray}となります。 $y'=0$ とすると $x=\pm 1$ ですね。もう一度微分すると \begin{eqnarray} y^{\prime\prime} &=& \frac{2}{x^3} \end{eqnarray}となります。

$\def\EtoN{\class{EtoN}{} }\def\EtoS{\class{EtoS}{} }\def\NtoE{\class{NtoE}{} }\def\StoE{\class{StoE}{} }$$\require{cancel}$定義域は $x\ne 0$ なので、増減表は次のようになります。
\begin{array}{c|ccccccc} x & \cdots & -1 & \cdots & 0 & \cdots & 1 & \cdots \\ \hline y' & + & 0 & - & / & - & 0 & + \\ \hline y^{\prime\prime} & - & - & - & / & + & + & + \\ \hline y & \NtoE & -2 & \EtoS & / & \StoE & 2 & \EtoN \end{array}$x=-1$ のときに極大値 $-2$ をとり、 $x=1$ のときに極小値 $2$ をとることがわかります。

この増減表をもとにグラフをかきたいのですが、定義域の境目や端っこ、つまり、 $x=0$ や $x\to\pm\infty$ で、どのようになっているかを考える必要があります。

まず、 $x\to +0$ を考えると、 $y=x+\dfrac{1}{x}$ の1項目が $0$ に収束し、2項目は $\infty$ へ発散するので、 $y\to\infty$ となることがわかります。同様に、 $x\to -0$ のときは、 $y\to -\infty$ となります。どちらの場合も、グラフでいうと、 $y$ 軸に近づいていくことがわかります。

$x\to\infty$ のときは、 $y=x+\dfrac{1}{x}$ の1項目が $\infty$ へ発散し、2項目は $0$ に収束するのだから、 $y\to\infty$ となることがわかります。同様に、 $x\to -\infty$ のときは、 $y\to -\infty$ となります。

この場合も、先ほどの $x\to \pm 0$ のときと同じように、ある直線に近づきます。それは式をよく見ればわかるでしょう。 $y=x+\dfrac{1}{x}$ の2項目は、 $x\to\pm\infty$ のときには $0$ に近づくので、この曲線は、直線 $y=x$ に近づいていくことがわかります。

以上から、この曲線の漸近線は、 $y$ 軸と、直線 $y=x$ であることがわかります。これと先ほどの増減表から、グラフは次のように書くことができます。

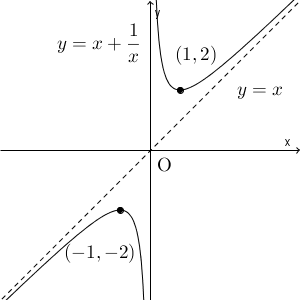
漸近線

漸近線とは、曲線がある直線に近づいていくときの、その直線のことを指します。先ほどの問題では漸近線を考えるのは難しくなかったですが、一般的にはどのように求めればいいでしょうか。

まず、漸近線が $x$ 軸に平行なとき、例えば、直線 $y=a$ となるのはどのようなときでしょうか。これは曲線の右端か左端が $a$ に近づいていけばいいので、\[ \lim_{x\to\infty} f(x)=a,\ \lim_{x\to-\infty} f(x)=a \]の少なくともどちらか一方が成り立つときだと考えられます。このように、式で考えて漸近線を求めることができるようになります。特に、 $a=0$ なら、 $x$ 軸が漸近線、ということです。

次に、漸近線が $y$ 軸に平行なとき、例えば、直線 $x=b$ となるのはどのようなときでしょうか。イメージとしては、 $y=\tan x$ のグラフと $x=\dfrac{\pi}{2}$ を考えるといいでしょう。漸近線が $x=b$ となるのは、
\begin{eqnarray} & & \lim_{x\to b-0} f(x)=\infty,\ \lim_{x\to b-0} f(x)=-\infty \\[5pt] & & \lim_{x\to b+0} f(x)=\infty,\ \lim_{x\to b+0} f(x)=-\infty \\[5pt] \end{eqnarray}の少なくともどれか1つが成り立つときです。

最後に、直線 $y=ax+b$ に近づくときはどのようなときでしょうか。これは直線との差がどんどんなくなっていく、と考えれば、
\begin{eqnarray} & & \lim_{x\to\infty} \{f(x)-(ax+b)\}=0　\\[5pt] & & \lim_{x\to-\infty} \{f(x)-(ax+b)\}=0 \end{eqnarray}の少なくともどちらかが成り立つときです。先ほどの例題では、\[ \lim_{x\to\infty} \left\{\left(x+\dfrac{1}{x}\right)-x\right\}=0 \]となったので、直線 $y=x$ が漸近線だと言えたわけですね。