【基本】一次分数関数のグラフ
ここでは、一次分数関数のグラフがどうなるかを見ていきます。見慣れた形が出てきます。
もっともシンプルな例
【基本】一次分数関数で見たように、一次分数関数とは、\[ y=\dfrac{ax+b}{cx+d} \]で表されるものを言います。ただし、 $c\ne0$, $ad-bc\ne0$ とします。
こうした一次分数関数の式の中で、一番シンプルなものは、 $a=0$, $d=0$ とした場合でしょう。 $k=\dfrac{b}{c}$ とおけば、\[ y=\dfrac{k}{x} \]となります。これは、すでに見たことがある式です。反比例ですね。グラフは、次のように双曲線になります。
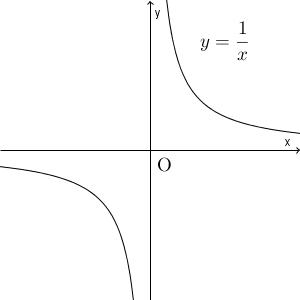
上のグラフは、 $y=\dfrac{1}{x}$ のグラフです。 $k$ が正の場合であれば、上のグラフのように、右上と左下に曲線が現れます。負の場合であれば、左上と右下に現れます。
曲線がある直線に近づいていく場合、その直線のことを漸近線(漸近線、asymptote) といいます。 $k$ が正の場合でも負の場合でも、漸近線は $x$ 軸と $y$ 軸になります。このように、漸近線が直交するような双曲線は、直角双曲線と呼ばれています。
この場合は問題ないでしょう。
もっともシンプルな例を平行移動する
$y=\dfrac{k}{x}$ を、 $x$ 軸方向に $p$, $y$ 軸方向に $q$ だけ平行移動したものを考えましょう。
平行移動前の点を $(X,Y)$ と書き、平行移動後の点を $(x,y)$ と書くと、 $x=X+p$, $y=Y+q$ が成り立ちます。平行移動前は\[ Y=\dfrac{k}{X} \]が成り立っているので、ここに $X=x-p$, $Y=y-q$ を代入すると
\begin{eqnarray}
y-q &=& \dfrac{k}{x-p} \\[5pt]
y &=& \dfrac{k}{x-p}+q \\[5pt]
&=& \dfrac{qx+(k-pq)}{x-p} \\[5pt]
\end{eqnarray}となります。最後の式を見ると、一次分数関数の形になっていますね。なので、平行移動後のグラフは、一次分数関数のグラフになっていることがわかります。
平行移動したことからもわかりますが、\[ y=\dfrac{k}{x-p}+q \]のグラフは、双曲線であり、漸近線が $x=p$ と $y=q$ の2直線であることがわかります。また、定義域は $x\ne p$ となります。 $y=q$ となることはないので、値域は、 $y\ne q$ となります。
一般の一次分数関数のグラフ
先ほどは、「 $y=\dfrac{k}{x}$ のグラフを平行移動すれば、一次分数関数のグラフが得られる」という話をしましたが、一次分数関数 $y=\dfrac{ax+b}{cx+d}$ のすべての場合をカバーできているかどうかは、明らかではないですね。式変形をして、少し確かめてみましょう。
\begin{eqnarray} y &=& \dfrac{ax+b}{cx+d} \\[5pt] &=& \dfrac{\frac{a}{c}x+\frac{b}{c} }{x+\frac{d}{c} } \\[5pt] &=& \dfrac{\frac{a}{c}\left(x+\frac{d}{c}\right)-\frac{ad}{c^2}+\frac{b}{c} }{x+\frac{d}{c} } \\[5pt] &=& \dfrac{a}{c}+\dfrac{-\frac{ad}{c^2}+\frac{b}{c} }{x+\frac{d}{c} } \\[5pt] &=& \dfrac{a}{c}+\dfrac{\frac{1}{c^2}(-ad+bc)}{x+\frac{d}{c} } \\[5pt] \end{eqnarray}となります。 $c\ne 0$ なので、こうした変形ができます。また、 $ad-bc\ne0$ なので、最後の項が $0$ でないこともわかります。この式を見ると、 $k=\dfrac{1}{c^2}(-ad+bc)$, $p=-\dfrac{d}{c}$, $q=\dfrac{a}{c}$ とすれば、 $y=\dfrac{ax+b}{cx+d}$ のグラフが $y=\dfrac{k}{x}$ のグラフを $x$ 軸方向に $p$, $y$ 軸方向に $q$ だけ平行移動したものなる、ということができるようになります。
この式は覚える必要はありません。具体的な変形は、【基本】一次分数関数#一次分数関数の変形で見たように、式を割り算するだけです。上とほとんど同じ計算をすることになりますが、具体的なほうがだいぶ計算はしやすいです。
具体的な例で見てみましょう。 $y=\dfrac{4x+5}{2x+5}$ のグラフをかけと言われたら、
\begin{eqnarray}
y
&=&
\dfrac{4x+5}{2x+5} \\[5pt]
&=&
\dfrac{2(2x+5)-5}{2x+5} \\[5pt]
&=&
2-\dfrac{5}{2x+5} \\[5pt]
&=&
2-\dfrac{\frac{5}{2} }{x-\left(-\frac{5}{2}\right)} \\[5pt]
\end{eqnarray}となります。よって、 $y=-\dfrac{5}{2x}$ のグラフを、 x 軸方向に $-\dfrac{5}{2}$, y 軸方向に $2$ だけ平行移動したグラフをかけばいいんだな、ということがわかります。「 $x$ 軸方向に $-5$ 」ではないことに注意しましょう。
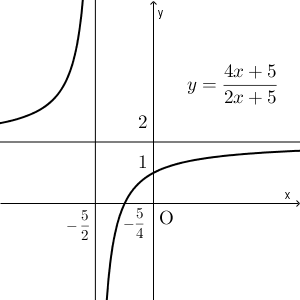
手書きでかく場合は、漸近線が $x=-\dfrac{5}{2}$, $y=2$ になることに注意します。また、 $x$ 軸や $y$ 軸との交点の座標はかいておくといいでしょう。
おわりに
ここでは、一次分数関数のグラフについて見ました。どのような場合でも、双曲線になるんですね。式変形をして、どのように平行移動すればいいのかを考えられるようにしておきましょう。





