【標準】一次分数関数のグラフ
ここでは、一見すると一次分数関数のようには見えないけれど、実は一次分数関数、というものを見ていきます。そのグラフのかき方も見ていきます。
一次分数関数のグラフ1
一見すると一次分数関数には見えませんが、 $y=$ の形に変形していくと、一次分数関数であることがわかります。変形していきましょう。
\begin{eqnarray}
2xy+x+4y-3 &=& 0 \\[5pt]
(2x+4)y &=& -x+3 \\[5pt]
\end{eqnarray}ここで、 $2x+4$ で両辺を割れば、一次分数関数の形となります。しかし、注意が必要なのは、 $2x+4$ が $0$ になることはないのか、という点です。もしそうなる場合があれば、 $0$ になる場合とならない場合で分けて考えなければいけません。
今の場合、 $2x+4=0$ とすると、 $x=-2$ となります。このとき、\[ (2x+4)y=-x+3 \]は左辺が $0$ で右辺は $5$ となるため、これを満たす $(x,y)$ がないことがわかります。そのため、 $x\ne -2$ であることがわかります。
このことから、 $2x+4$ で両辺を割ることができるので
\begin{eqnarray}
(2x+4)y &=& -x+3 \\[5pt]
y &=& \frac{-x+3}{2x+4} \\[5pt]
&=& \frac{-\frac{1}{2}(2x+4)+5}{2x+4} \\[5pt]
&=& -\frac{1}{2}+\frac{5}{2x+4} \\[5pt]
\end{eqnarray}と変形できます。 $\dfrac{5}{2x+4}=\dfrac{5}{2(x+2)}$ なので、このグラフは $y=\dfrac{5}{2x}$ を $x$ 軸方向に $-2$, $y$ 軸方向に $-\dfrac{1}{2}$ だけ平行移動したものとなります。
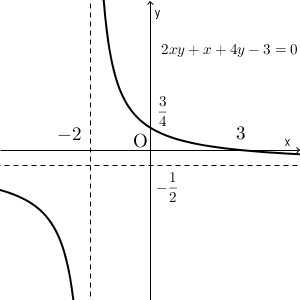
グラフは上のようになります。漸近線は、 $x=-2$, $y=-\dfrac{1}{2}$ の2直線となります。
一次分数関数のグラフ2
これも、 $y=$ の形にしてみるまでは、一次分数関数だとはわかりにくいですね。同じように $y=$ と変形していきたくなります。
その前に、分母が $0$ となる点を除いておきましょう。与えられた式の分母が $0$ になることはないので、 $x\ne 0$, $y\ne 0$ となります。この条件は後で使います。これを忘れないようにして、式を変形していきましょう。
\begin{eqnarray} \frac{1}{x}+\frac{1}{y} &=& 1 \\[5pt] y+x &=& xy \\[5pt] (1-x)y &=& -x \\[5pt] \end{eqnarray}となります。ここで、 $x=1$ とすると、最後の式は $0=-1$ となってしまうので、 $x\ne 1$ であることがわかります。よって、両辺を $1-x$ で割って \begin{eqnarray} y &=& \frac{-x}{1-x} \\[5pt] &=& \frac{x}{x-1} \\[5pt] &=& 1+\frac{1}{x-1} \\[5pt] \end{eqnarray}と変形することができます。よって、この関数のグラフは、 $y=\dfrac{1}{x}$ を $x$ 軸方向に $1$, $y$ 軸方向に $1$ だけ平行移動したグラフから原点を除いたもの、となります。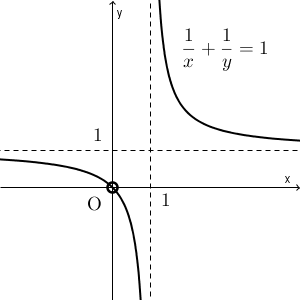
先ほども見たように、もとの式の形から $x=0$ となる点と $y=0$ となる点は除く必要がありますが、今の場合、原点だけが対象になります。そのため、原点を除いたものが、求めるグラフとなります。
漸近線は、 $x=1$, $y=1$ の2直線となります。
おわりに
ここでは、一次分数関数の形に変形してからグラフをかく問題を考えました。分母が $0$ になる点を除くことを忘れないようにしましょう。
また、一次分数関数の分母が、 $2x+4$ などとなっていたときに、「 $x$ 軸方向に $4$ だけ平行移動」とか「 $x$ 軸方向に $-4$ だけ平行移動」などとしてしまわないように注意しましょう。「 $x$ 軸方向に $-2$ だけ平行移動」が正しい内容です。





