【標準】一次分数関数のグラフと不等式
ここでは、不等式の問題で、一次分数関数のグラフが利用できるものを見ていきます。
一次分数関数と不等式
左辺が分数なのでやっかいですね。なので、両辺に $2-x$ を掛けたくなります。しかし、 $2-x$ は正とは限らないので、掛けてしまうと不等号の向きがどうなってしまうかわかりません。
なので、 $2-x$ を両辺に掛けるまえに、 $x\gt 2$ のときと $x\lt 2$ のときで分けてから解く、という方法をとることがまず考えられます。
また、もう1つの解法として、両辺に $(2-x)^2$ を掛ける、という方法もあります。これだと 0以上の値を掛けることが確定しているので、場合分けをする必要はありません。しかし、右辺は三次関数になってしまいます。そのため、不等式を解くには三次関数のグラフをかく必要が出てきます。
ここでは、これら2つの解法ではなく、一次分数関数のグラフを利用した方法で解くことにしましょう。つまり、 $y=\dfrac{3x-2}{2-x}$ と $y=x$ の2つのグラフを比較して解く、ということです。
$y=\dfrac{3x-2}{2-x}$ のグラフをかきましょう。そのために、次のように変形します。
\begin{eqnarray}
y
&=&
\frac{3x-2}{2-x} \\[5pt]
&=&
\frac{-3(2-x)+4}{2-x} \\[5pt]
&=&
-3+\frac{4}{2-x} \\[5pt]
&=&
-3-\frac{4}{x-2} \\[5pt]
\end{eqnarray}となります。このことから、 $y=\dfrac{3x-2}{2-x}$ のグラフは、 $y=-\dfrac{4}{x}$ のグラフを、 $x$ 軸方向に $2$, $y$ 軸方向に $-3$ だけ平行移動したものであることがわかります。
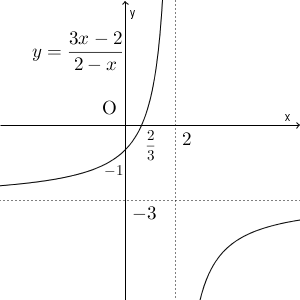
次に、直線 $y=x$ のグラフも追加します。

この2つのグラフは、2点で交わります。交点の $x$ 座標は
\begin{eqnarray}
\frac{3x-2}{2-x} &=& x \\[5pt]
3x-2 &=& x(2-x) \\[5pt]
x^2+x-2 &=& 0 \\[5pt]
(x+2)(x-1) &=& 0 \\[5pt]
x &=& 1,-2 \\[5pt]
\end{eqnarray}となります。よって、交点は $(1,1)$ と $(-2,-2)$ の2点であることがわかります。

これらを踏まえ、 $\dfrac{3x-2}{2-x} \leqq x$ となる範囲を考えましょう。それは、双曲線の左上の一部分と、右下の部分全体であることがわかります。よって、グラフから\[ -2\leqq x \leqq 1,\quad x\gt 2 \]であることがわかります。定義域に $x=2$ が含まれないため、解から除くことに注意しましょう。
別の方法で解く
先ほどの問題\[ \frac{3x-2}{2-x} \leqq x \]を、別の方法でも解いてみましょう。
まずは、 $2-x$ を掛ける方法です。 $x\lt 2$ の場合、 $2-x\gt 0$ なので、両辺に $2-x$ を掛けて
\begin{eqnarray}
3x-2 \leqq x(2-x) \\[5pt]
x^2+x-2 \leqq 0 \\[5pt]
(x+2)(x-1) \leqq 0 \\[5pt]
\end{eqnarray}となり、 $-2\lt x \lt 1$ となります。これは、 $x\lt 2$ を満たすので、全体が解となります。
また、 $x\gt 2$ の場合は、 $2-x\lt 0$ なので、
\begin{eqnarray}
3x-2 \geqq x(2-x) \\[5pt]
(x+2)(x-1) \geqq 0 \\[5pt]
\end{eqnarray}となり、 $x\geqq 1, x\leqq -2$ となります。このうち、 $x\gt 2$ を満たす範囲は、 $x\gt 2$ です。これが解となります。
以上から、2つの場合を合わせて、\[ -2\leqq x \leqq 1,\quad x\gt 2 \]と求められます。
続いて、 $(2-x)^2$ を掛ける方法です。この解き方では、両辺に正の値を掛けるため、場合分けは不要です。
\begin{eqnarray}
(3x-2)(2-x) \leqq x(2-x)^2 \\[5pt]
-3x^2+8x-4 \leqq x^3-4x^2+4x \\[5pt]
x^3-x^2-4x+4 \geqq 0 \\[5pt]
(x-1)(x^2-4) \geqq 0 \\[5pt]
(x-1)(x-2)(x+2) \geqq 0 \\[5pt]
\end{eqnarray}となります。 $y=(x-1)(x-2)(x+2)$ は次のようになります。
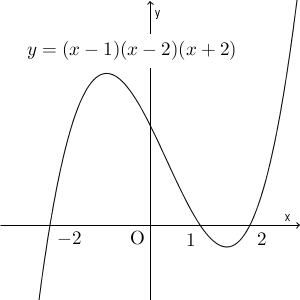
このことと、定義域に $x=2$ が含まれないことから、\[ -2\leqq x \leqq 1,\quad x\gt 2 \]が解だと求められます。
おわりに
ここでは、一次分数関数のグラフを用いて不等式を解く問題を考えました。分母に文字がある場合は、分母を取っ払いたくなりますが、一次分数関数のグラフがかける今となっては、分数関数のまま考えることもできます。
他の方法でも解くことはできますが、分母が $0$ になる場合を除くことを忘れないようにしましょう。





