【基本】三角関数のグラフ

🕒 2018/04/24 🔄 2023/05/01

ここでは、 $\sin\theta$, $\cos\theta$, $\tan\theta$ のグラフについて見ていきます。

📘 目次

sinθのグラフ

$y=\sin\theta$ のグラフをかいてみましょう。横が角度で、縦がそのときの $\sin$ を表す、というグラフです。

$\theta$ が $0$, $\dfrac{1}{6}\pi$, $\dfrac{1}{4}\pi$, $\dfrac{1}{3}\pi$, $\dfrac{1}{2}\pi$ のときなど、値が具体的にわかる値を元に点をとり、間をつなげていくと次のようになります。

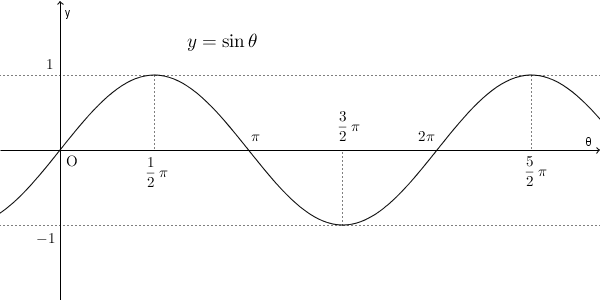
グラフは上のようになります。波のような形をしていますね。この形をした曲線のことを、正弦曲線やサインカーブ(sine curve)と呼びます。

なお、ときどき、単位円のグラフを三角関数のグラフと勘違いする人がいます。三角関数のグラフとは、横軸が角度を表し、縦軸が三角関数の値を表すものです。単位円のグラフは、角度と $\sin$ との対応を表していますが、横軸が角度を表しているわけではないので、単位円のグラフは三角関数のグラフではありません。

cosθのグラフ

続いて、 $y=\cos\theta$ のグラフをかいてみます。 $\sin$ のときと同じように、値がわかる点をもとにかくと、つぎのようになります。

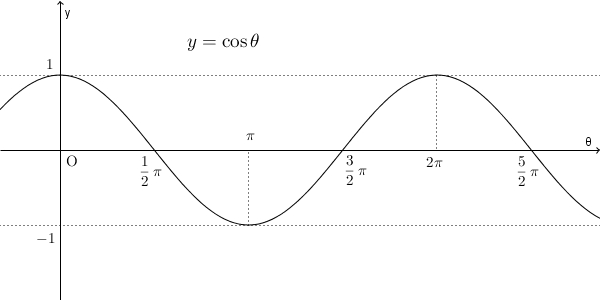
グラフは上のようになります。 $\sin$ のときと似ていますね。実は、 $y=\sin\theta$ のグラフを左へ $\dfrac{\pi}{2}$ だけずらすと、 $y=\cos\theta$ になります。そのため、 $y=\cos\theta$ のグラフも正弦曲線といいます。

tanθのグラフ

最後に、 $y=\tan\theta$ のグラフをかいてみましょう。同じように、値の分かる点をもとにかきますが、今度は今までとまったく違う形のグラフになります。

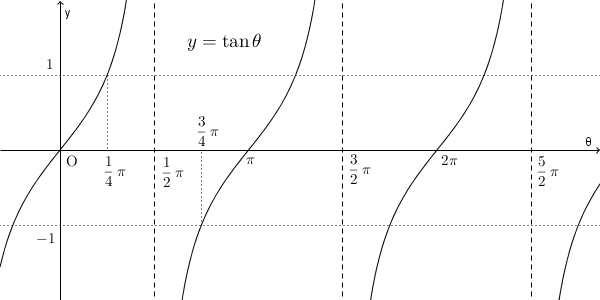
もともと、 $\tan$ は傾きを表していたので、 $\theta$ を $0$ から $\dfrac{1}{2}\pi$ に近づいていくと、値はどんどん大きくなります。そのため、上のように、グラフは $\theta=\dfrac{1}{2}\pi$ に近づいていきます。

このように、グラフがある直線に限りなく近づくとき、その直線をそのグラフの漸近線(asymptote) といいます。上のグラフからもわかる通り、 $y=\tan\theta$ の漸近線は次のようになります（n は整数）。\[ \theta=\dfrac{1}{2}\pi+n\pi \]

三角関数の周期性

【基本】一般角の三角関数と鋭角の三角関数で見たように、\[ \sin(\theta+2n\pi) = \sin\theta \]がすべての整数 n に対して成り立ちます。これはグラフでいうと、横に $2\pi$ だけずらすと、グラフが元のグラフと一致する、ということを表しています。つまり、同じ形が繰り返されているということですね。

このように、グラフが同じ形を繰り返すような関数を周期関数(periodic function) といいます。

$y=\sin\theta$ や $y=\cos\theta$ のグラフを見ると、同じ形が $2\pi$ ごとに繰り返されています。この繰り返す幅のことを周期(period) といいます。なので、「 $y=\sin\theta$ や $y=\cos\theta$ は、周期が $2\pi$ の周期関数」といいます。

なお、周期は $4\pi$ や $6\pi$ などとも考えられますが、通常、周期は、正で最小のものを指すことが多いです。

$y=\tan\theta$ のグラフも $2\pi$ ごとに同じ形をしていますが、よく見ると $\pi$ ごとに同じ形が繰り返されていますね。これは先ほどのリンク先で見た通り、\[ \tan(\theta+\pi)=\tan\theta \]が成り立つことからもわかります。このことから、「 $y=\tan\theta$ は、周期が $\pi$ の周期関数」といいます。

三角関数の対称性

$y=\cos\theta$ のグラフは、 $y$ 軸について対称ですね。これは、【基本】一般角の三角関数と鋭角の三角関数で見たように、\[ \cos(-\theta)=\cos\theta \]が成り立つことからもわかります。このような関数を偶関数(even function) といいます。

一方、 $y=\sin\theta$ や $y=\tan\theta$ のグラフは、原点について対称です。これは先ほどのリンク先で見た通り、\[ \sin(-\theta)=-\sin\theta, \tan(-\theta)=-\tan\theta \]が成り立つことからもわかります。このような関数を奇関数(odd function) といいます

なお、偶関数は、 x の偶数乗のグラフが $y$ 軸について対称であることに由来しています。奇関数は、 x の奇数乗のグラフが原点について対称であることに由来しています。