【応用】三角関数を含む等式・不等式(変域が変わる)
ここでは、変域が変わる場合の、三角関数を含む等式や不等式について見ていきます。
三角関数を含む等式
角が $\theta$ ではなく、 $\theta+\dfrac{\pi}{3}$ となっていますね。このままだと考えづらいので、 $\alpha=\theta+\dfrac{\pi}{3}$ とおいて考えることにしましょう。こうすると
\begin{eqnarray}
\sin\alpha &=& \dfrac{1}{\sqrt{2} } \\[5pt]
\end{eqnarray}と変形できるので、 $\alpha$ が求められそうですよね。
ただ、注意が必要なのは、 $\alpha$ の変域です。例えば、 $\alpha=\dfrac{\pi}{4}$ は解になりそうな気がしますが、このときに対応する $\theta$ は\[ \frac{\pi}{4}-\frac{\pi}{3}=-\dfrac{\pi}{12} \]となり、今考えている範囲の外になってしまいます。
【標準】三角関数を含む関数の最大・最小(相互関係利用)でも出てきますが、別の文字で置き換えるときには、変域がどう変わるかも考えておかなくてはいけません。今の場合は、 $\alpha=\theta+\dfrac{\pi}{3}$ なので、\[ \dfrac{\pi}{3}\leqq \alpha\lt\dfrac{7\pi}{3} \]という範囲になります。単位円で考えると、次のようになります。

$\left(\dfrac{1}{2},\dfrac{\sqrt{3} }{2}\right)$ から出発して反時計回りに一周するという、この少し変わった範囲で、 $\sin$ の値が $\dfrac{1}{\sqrt{2} }$ になるものを考えないといけません。これより、\[ \alpha=\dfrac{3}{4}\pi,\dfrac{9}{4}\pi \]であることがわかります。 $\theta=\alpha-\dfrac{\pi}{3}$ だから\[ \theta=\frac{5}{12}\pi,\frac{23}{12}\pi \]が答えとなります。
三角関数を含む不等式
不等式の場合でも、角を分かりやすく置き換えて考えます。先ほどと同じように、範囲に注意して考えていきます。
$\alpha=2\theta-\dfrac{1}{4}\pi$ とすると、$\alpha$ の値のとりうる範囲は\[ -\frac{1}{4}\pi \leqq \alpha \lt 4\pi-\frac{1}{4}\pi \]となります。
また、不等式は\[ \cos\alpha\gt\frac{1}{2} \]なので、今考えている範囲では、3か所が該当することになります。わかりやすいように、場合分けをして書いてみます。
まず、 $-\dfrac{1}{4}\pi \leqq \alpha \lt \dfrac{3}{2}\pi$ の範囲で考えてみます。 $\dfrac{3}{2}\pi$ に特に意味はなく、途中で範囲を切りたかっただけです。他の切り方でも構いません。この範囲で区切ると、下の赤い部分が該当します。
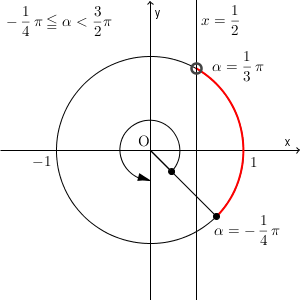
次に、 $\dfrac{3}{2}\pi \leqq \alpha \lt 2\pi+\dfrac{3}{2}\pi$ の範囲で考えてみると、このときは下の部分が該当します。
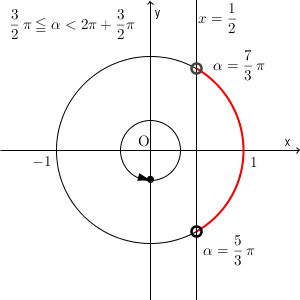
最後に、 $2\pi+\dfrac{3}{2}\pi \leqq \alpha \lt 4\pi-\dfrac{1}{4}\pi$ の範囲を考えます。このときは、下の部分が該当します。

以上から、 $-\dfrac{1}{4}\pi\leqq \alpha\lt\dfrac{1}{3}\pi$, $\dfrac{5}{3}\pi\lt \alpha\lt\dfrac{7}{3}\pi$, $\dfrac{11}{3}\pi\lt \alpha\lt\dfrac{15}{4}\pi$ の3つの範囲が該当します。 $-\dfrac{1}{4}\pi$ の部分にだけイコールがつくことに注意しましょう。
$\theta=\dfrac{1}{2}\left(\alpha+\dfrac{1}{4}\pi\right)$ なので、 $\theta$ の範囲は、 $0\leqq \theta\lt\dfrac{7}{24}\pi$, $\dfrac{23}{24}\pi\lt \theta\lt\dfrac{31}{24}\pi$, $\dfrac{47}{24}\pi\lt \theta\lt 2\pi$ となります。これが答えです。
おわりに
ここでは、三角関数を含む等式や不等式を解くときに、変域が変わるような問題を見ました。角を他の文字で置くときに、変域がどのように変わるかに注意し、新しい変域で等式・不等式を解かなくてはいけません。特に、不等式では、範囲が複雑になりやすく、細かな分数の計算も出てくるので、注意して考えるようにしましょう。





