【標準】三角関数を含む不等式

ここでは、三角関数を含む不等式について見ていきます。

三角関数を含む不等式

$\sin\theta=\dfrac{1}{2}$ を解く、といった方程式の問題は、【標準】三角関数の値で見ました。単位円をかいて考えましたね。

方程式ではなく、不等式の場合も、単位円をかいて考えます。ただし、範囲にはよく注意して考えていく必要があります。

(1)の $\sin\theta\leqq -\dfrac{1}{2}$ について考えましょう。単位円をかいて、まずは、 y 座標が $-\dfrac{1}{2}$ となるところを特定しましょう。

上の図から、 $\theta=\dfrac{7}{6}\pi$, $\dfrac{11}{6}\pi$ であることがわかります。求める範囲は、 y 座標が $-\dfrac{1}{2}$ 以下の部分ですね。なので、上の赤い部分が該当します。よって、\[
\frac{7}{6}\pi\leqq \theta \leqq\frac{11}{6}\pi \]が求める範囲となります。

このように、三角関数を含む不等式を解くには、単位円をかいて、境目となる部分を考えてから、範囲を求める、というのが基本的な流れです。

続いて、(2)の $\cos\theta\gt \dfrac{1}{2}$ を考えます。単位円をかいて、 x 座標が $\dfrac{1}{2}$ の部分を考えます。

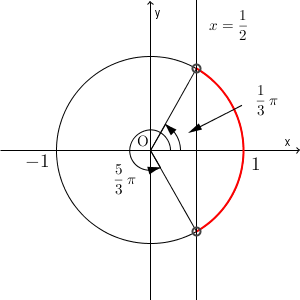
上の図から、 $\theta=\dfrac{1}{3}\pi$, $\dfrac{5}{3}\pi$ であることがわかります。求める範囲は、 x 座標が $\dfrac{1}{2}$ より大きい部分なので、上の赤い部分が該当しますが、(1)のときと違って、答え方が少しわかりにくいですね。

もともと、 $\theta=0$ に対応するのが $(1,0)$ でした。そこから反時計回りに一周した範囲が、 $0\leqq \theta\lt 2\pi$ となります。なので、上の赤い部分は、1つにつながっていますが、答えるときは $x$ 軸で2つに分割して答えることになります。\[ 0\leqq \theta\lt \frac{1}{3}\pi,\ \frac{5}{3}\pi\lt\theta\lt 2\pi \]が答えです。 $0$ の部分にイコールが入っていることに注意しましょう。

ちなみに、もし(2)の問題が $\cos\theta\geqq \dfrac{1}{2}$ だったとしたら、答えは次のように変わります。\[ 0\leqq \theta\leqq \frac{1}{3}\pi,\ \frac{5}{3}\pi\leqq \theta\lt 2\pi \]イコールのついている位置に注意しましょう。

最後に、(3)の $\tan\theta\geqq 1$ について考えます。まずは、単位円をかいて、原点を通り、傾きが $1$ の直線をかいてみます。

上の図から、 $\tan\theta=1$ となるのは、 $\theta=\dfrac{1}{4}\pi$, $\dfrac{5}{4}\pi$ のときであることがわかります。さて、求めたいのは、傾きが $1$ 以上となるところですね。単位円上の点と原点とを結んだ直線が、 $1$ 以上の傾きとなる部分、言い換えれば、直線 $x=1$ との交点の y 座標が $1$ 以上となる部分を考えてみましょう。これは間違いやすいですが、下の図のようになります。

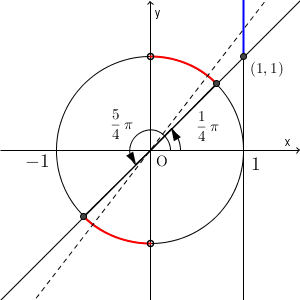
単位円上の点と原点との結んだ直線（例えば上の図の破線）が、直線 $x=1$ の $y\geqq 1$ の部分（上の図の青い線）と交わるような部分は、上の図の赤い線の部分となります。2か所に分かれるんですね。しかも、 $\theta=\dfrac{1}{2}\pi$, $\dfrac{3}{2}\pi$ のところでは、 $\tan\theta$ は定義されないので、除く必要があります。以上から、 $\tan\theta\geqq 1$ の解は\[ \frac{1}{4}\pi\leqq \theta\lt \frac{1}{2}\pi,\ \frac{5}{4}\pi\leqq \theta\lt \frac{3}{2}\pi \]が答えとなります。ここでも、イコールのついている場所に注意しましょう。 $\tan$ の場合は、 $\dfrac{1}{2}\pi+n\pi$ （n は整数）を除くことを忘れないようにしましょう。

おわりに

ここでは、三角関数を含む不等式について見てきました。方程式のときと同じように単位円をかいて考えます。単位円のどの部分が対応するか、よく見て答えるようにしましょう。