【基本】三角関数の相互関係

🕒 2018/04/22 🔄 2023/05/01

ここでは、三角関数の相互関係について見ていきます。

📘 目次

三角関数の復習

【基本】三角関数の定義では、一般角に対して三角関数を定義しました。 $\mathrm{ O }(0,0)$ を中心に $\mathrm{ A }(1,0)$ を反時計回りに $\theta$ だけ回転したときに、 $\mathrm{ P }(x,y)$ に移るとすると、\[ \sin\theta=y, \cos\theta=x,\tan=\dfrac{y}{x} \]となるのでした（ $x=0$ のとき、 $\tan$ は定義しない）。

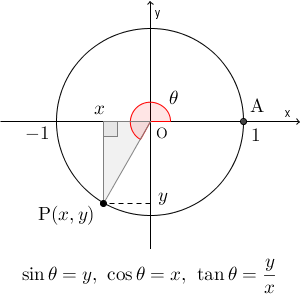
本来は、半径が $r$ の円を使って定義すべきですが、結局、後で座標を半径で割るため、はじめから半径 $1$ の円で考えればいいですね。

三角関数の相互関係

【基本】三角比の相互関係や【基本】三角比の相互関係（鈍角）で見たように、 $\sin$, $\cos$, $\tan$ は、それぞれ、関係式によって結びついていました。今までは、0度から180度の場合で考えていましたが、一般の角度に対しても成り立ちます。

まず、上で見た定義から、点 $(\cos\theta,\sin\theta)$ は、原点が中心で、半径が $1$ の円周上にあります。よって、\[ \sin^2\theta+\cos^2\theta=1 \]が成り立ちます。

また、 $\tan$ が傾きを表していることから、\[ \tan\theta=\frac{\sin\theta}{\cos\theta} \]が成り立つこともわかります。

これら2つを合わせれば、1つ目の式の両辺を $\cos^2\theta$ で割って、\[ 1+\tan^2\theta=\frac{1}{\cos^2\theta} \]が成り立つことがわかります。

以上から、0度から180度の場合に成り立っていた相互関係は、一般角に対しても成り立つことがわかります。

三角関数の相互関係

一般角 $\theta$ に対して、次が成り立つ。

$\displaystyle \tan\theta = \frac{\sin\theta}{\cos\theta}$
$\sin^2\theta +\cos^2\theta = 1$
$\displaystyle \tan^2\theta +1 = \frac{1}{\cos^2\theta}$

これらを使えば、三角関数の値のうち、1つが分かれば、他の2つも求めることができるようになります。

三角関数の値の符号

三角関数の相互関係を使う場合、符号に注意する必要があります。

0度から180度までの場合、 $\sin$ が負の値をとることはありませんでしたが、一般角の場合はそうではありません。冒頭で見た図で、 P の位置によって、 $\sin\theta$ の符号は次のように変わります。

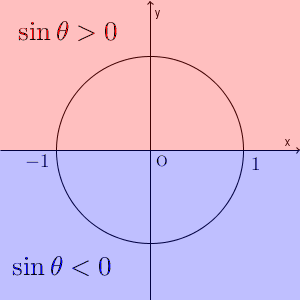
$\sin\theta$ は、第1象限・第2象限のときは正、第3象限・第4象限のときは負、となります。また、 $\cos\theta$ と $\tan\theta$ の符号は、次のようになります。

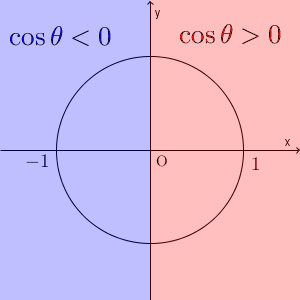
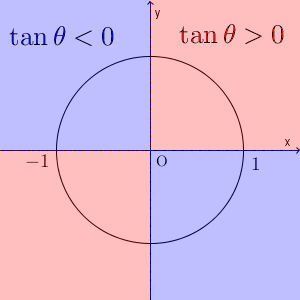
$\cos\theta$ は、第1象限・第4象限のときは正、第2象限・第3象限のときは負、となります。$\tan\theta$ は、第1象限・第3象限のときは正、第2象限・第4象限のときは負、となります。

$\sin$ は y 座標の符号を、 $\cos$ は x の符号を考えればいいですね。 $\tan$ は傾きが正か負かで考えればいいでしょう。

なお、 $\mathrm{ O }(0,0)$ を中心に $\mathrm{ A }(1,0)$ を反時計回りに $\theta$ だけ回転したとき、第1象限内の点に移動する場合、 $\theta$ を「第1象限の角」といいます。他の象限についても同じです。

三角関数の相互関係を使った問題

例題

$\tan\theta=-2$ のときに、 $\sin\theta$ と $\cos\theta$ を求めなさい。

今まで見た内容を踏まえて考えてみましょう。まず、符号を見れば、第2象限・第4象限の角であることがわかりますね。

$\tan$ と $\cos$ の関係式から、
\begin{eqnarray} 1+(-2)^2 &=& \frac{1}{\cos^2\theta} \\[5pt] \cos^2\theta &=& \frac{1}{5} \\[5pt] \cos\theta &=& \pm\frac{1}{\sqrt{5} } \\[5pt] \end{eqnarray}となります。また、 \begin{eqnarray} \sin\theta=\cos\theta\tan\theta \end{eqnarray}なので、\[ (\sin\theta,\cos\theta) = \left(\frac{2}{\sqrt{5} },-\frac{1}{\sqrt{5} }\right), \left(-\frac{2}{\sqrt{5} },\frac{1}{\sqrt{5} }\right) \]となります。

$\sin\theta$ を求めるときに、 $\sin^2\theta+\cos^2\theta=1$ を使う方法もありますが、この場合、 $\cos$ と $\sin$ の符号の関係が分からなくなってしまいます。つまり、例えば $\left(\dfrac{2}{\sqrt{5} },\dfrac{1}{\sqrt{5} }\right)$ も答えに含んでしまう、という間違いをする可能性があります。

こうした間違いを防ぐために、 $\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ が使えるときはこちらを優先して使うようにする、もしくは、どの象限の角かを最後に確認する、のどちらかを選びましょう。