【標準】三角関数のグラフ

ここでは、いろいろな三角関数のグラフについて見ていきます。

縦に変化する三角関数のグラフ

基本的な三角関数のグラフは、【基本】三角関数のグラフで見た通りです。これらを利用して、例題を考えていきましょう。

まず、 $2\sin\theta$ は、 $\sin\theta$ を2倍したものなので、 $y=\sin\theta$ のグラフを、 $\theta$ 軸を基準にして y 軸方向に2倍すればいいですね。グラフは次のようになります。

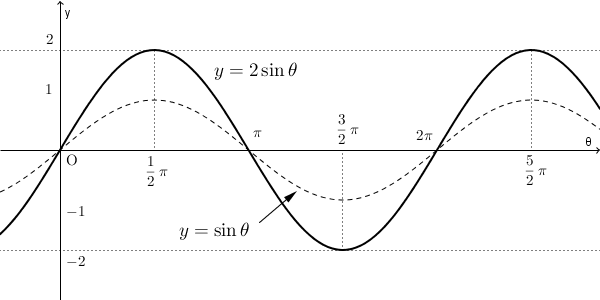
(2)の $y=1-\cos\theta$ は、順番に考えていきましょう。まず、 $-\cos\theta$ の部分を考えると、 $\cos\theta$ を $-1$ 倍したものなので、 $y=\cos\theta$ のグラフを上下反転させればいいですね。

さらにこれに $1$ を加えたものが $y=1-\cos\theta$ なので、上に $1$ だけ平行移動すれば求めたいグラフになります。

これが $y=1-\cos\theta$ のグラフとなります。

なお、上のリンク先では、周期も考えましたね。この例題のグラフは、基準となる $y=\sin\theta$ や $y=\cos\theta$ のグラフを上下に変化させているだけですね。周期は横に関する情報なので、変化しません。つまり、この例題の2つの関数の周期は、どちらも $2\pi$ となります。

横に変化する三角関数のグラフ

今度は、三角関数の外側ではなく、内側、つまり、 $\theta$ の部分が変わっています。三角関数の値を変化させるのではなく、角が変わっているので、先ほどとは違っていますね。具体的な角を入れて、基準のグラフと比較してどう変わるか、考えてみましょう。

$y=\tan2\theta$ に $\theta=0$, $\dfrac{\pi}{12}$, $\dfrac{\pi}{8}$, $\dfrac{\pi}{6}$ を入れて値を考えてみると、それぞれ $y=\tan\theta$ に $\theta=0$, $\dfrac{\pi}{6}$, $\dfrac{\pi}{4}$, $\dfrac{\pi}{3}$ を入れたときと同じ値になりますね。具体的な点で対応させると次のようになります。

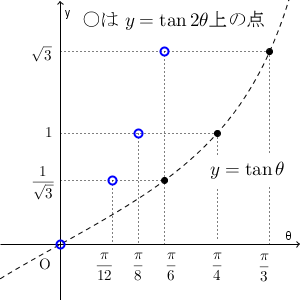
このことから、 $y=\tan2\theta$ のグラフは、 $y=\tan\theta$ のグラフを、 y 軸を基準として $\theta$ 軸方向に $\dfrac{1}{2}$ 倍にしたものになります。

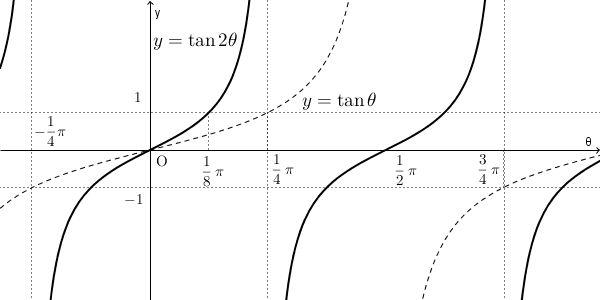
他の場合も同様で、例えば、 $k\ne0$ のとき、 $y=\sin k\ \theta$ のグラフは、 $y=\sin\theta$ のグラフを y 軸を基準として $\theta$ 軸方向に $\dfrac{1}{k}$ 倍にしたものになります。 $\theta$ に k が掛かっているので k 倍になると思いがちですが、逆なんですね。変化後のグラフの $\dfrac{1}{k}\theta$ のときが、変化前のグラフの $\theta$ と対応することになります。

(2)も、具体的な値で考えてみましょう。 $y=\sin\left(\theta-\dfrac{1}{6}\pi\right)$ に $\theta=0$, $\dfrac{\pi}{6}$, $\dfrac{\pi}{3}$, $\dfrac{2\pi}{3}$ を入れて、値を考えてみると、それぞれ $y=\sin\theta$ に $\theta=-\dfrac{\pi}{6}$, $0$, $\dfrac{\pi}{6}$, $\dfrac{\pi}{2}$ を入れたときと同じ値になりますね。具体的な点で対応させると次のようになります。

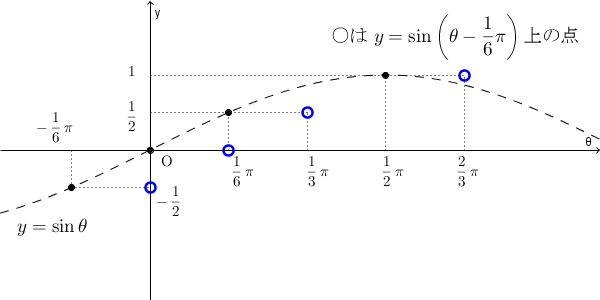
このことから、 $y=\sin\left(\theta-\dfrac{1}{6}\pi\right)$ のグラフは、 $y=\sin\theta$ のグラフを、 $\theta$ 軸方向に $\dfrac{1}{6}\pi$ だけ平行移動したものになります。

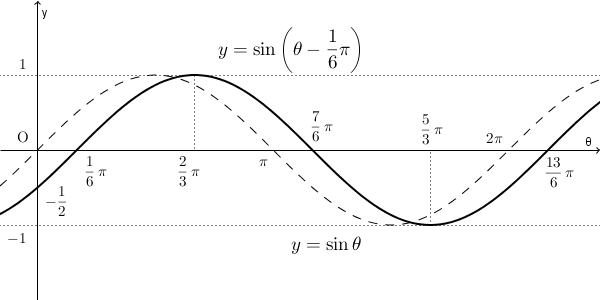
これも、 $-\dfrac{\pi}{6}$ とあるので、左に平行移動するように思いがちですが、逆です。平行移動後の $\theta=\dfrac{\pi}{6}$ のときが、平行移動前の $\theta=0$ に対応することからもわかる通り、平行移動後は右にずれていることがわかります。

なお、グラフの平行移動に関する一般的な話は、【発展】グラフの平行移動でも扱っています。

最後に、周期についても考えておきましょう。(1)は、横に $\dfrac{1}{2}$ 倍となっているため、周期も短くなります。もともと $\tan$ の周期は $\pi$ だったので、(1)の関数の周期は $\dfrac{1}{2}\pi$ となります。(2)は、平行移動しただけで、波の形は変わらないため、周期も変わらず、 $2\pi$ となります。

sinとcosのグラフ

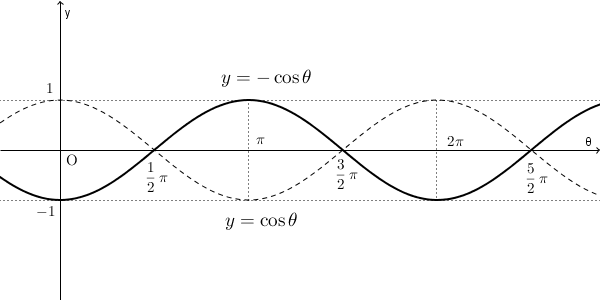
【基本】三角関数のグラフでは、 $y=\sin\theta$ と $y=\cos\theta$ のグラフは同じ形になり、どちらも正弦曲線と呼ぶ、と書きました。それは、【標準】一般角の三角関数と鋭角の三角関数の最後の部分で見た通り、\[ \cos\theta=\sin\left(\theta+\dfrac{1}{2}\pi\right) \]となることからわかります。このことから、 $y=\cos\theta$ のグラフは $y=\sin\theta$ のグラフを $\theta$ 方向に $-\dfrac{1}{2}\pi$ だけ平行移動したものである、ということがわかります。

おわりに

ここでは、縦や横に変化する三角関数のグラフについて見ました。横に変化する三角関数のグラフは少し難しいですね。具体的な点をとって、基準となるグラフをどのように変化させればいいかを考えるようにすると間違いにくいでしょう。