【基本】複素数平面と内分点・外分点

ここでは、複素数平面上で、内分点・外分点について考えていきます。

複素数の演算と複素数平面との対応についての復習

複素数の四則演算などの演算は、複素数平面上では、いろいろな移動に対応するのでした。

複素数の加算・減算は、複素数平面上では、平行移動に対応します（参考：【基本】複素数平面と複素数の加法・減法・実数倍）。

複素数の乗法・除法は、複素数平面上では、拡大・縮小と回転に対応します（参考：【基本】複素数の極形式と積、【基本】複素数の極形式と商）。どれだけ拡大・縮小するか、どれだけ回転するかは、それぞれ、複素数の絶対値と偏角に対応します。これらを把握するために、極形式という表し方があるのでした。

四則演算以外にも、移動に対応するものがあります。共役複素数は、複素数平面上では、実軸に対する対称移動に対応しています（参考：【基本】複素数平面と共役複素数）。

このように、複素数平面で考えると、複素数の計算によって、図形を扱えるようになります。場合によっては、図形の性質を使ったり、平面座標や三角関数やベクトルなどを使うよりも、ずっと扱いやすくなることもあります。

ここからは、複素数平面で、図形を扱う方法について見ていきます。

線分の内分点・外分点

まずは、点の表し方です。

複素数平面上で、 $\mathrm{ A }(\alpha)$, $\mathrm{ B }(\beta)$ に対し、線分 AB を $m:n$ に内分する点 C がどのような複素数に対応するかを考えてみましょう。

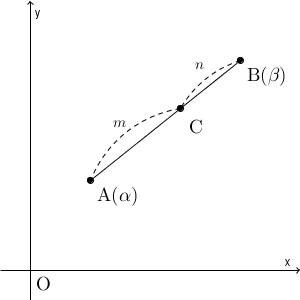
これは、実部・虚部にわけて考えるとわかりやすいです。 $\alpha=a+bi$, $\beta=c+di$ とすると、普通の座標平面のときと同じように計算できます（参考：【基本】平面上での内分点と外分点）。点 C の実部と虚部は、それぞれ\[ \frac{na+mc}{m+n},\ \frac{nb+md}{m+n} \]となります。これより、点 C に対応する複素数は
\begin{eqnarray} & & \frac{na+mc}{m+n}+\frac{nb+md}{m+n}i \\[5pt] &=& \frac{n(a+bi)+m(c+di)}{m+n} \\[5pt] &=& \frac{n\alpha+m\beta}{m+n} \\[5pt] \end{eqnarray}となります。外分のときも、座標平面のときの結果を利用して同じように計算して、次が成り立つことがわかります。

中点と重心

内分点・外分点の中でも、一番よく登場するのは、中点です。中点は、 $1:1$ に内分する点といえるので $\dfrac{\alpha+\beta}{2}$ で表すことができます。

これを踏まえて、三角形の重心について考えてみましょう。

複素数平面上の3点 $\mathrm{ A }(\alpha)$, $\mathrm{ B }(\beta)$, $\mathrm{ C }(\gamma)$ を頂点とする三角形があるとしましょう。この重心に対応する複素数を求めてみます。

重心とは、【基本】三角形の重心でも見た通り、中線を $2:1$ に内分する点です。 BC の中点を D とすると、線分 AD を $2:1$ に内分する点が、三角形 ABC に重心になります。

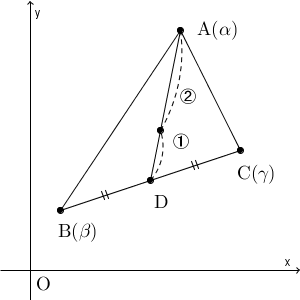
BC の中点 D は、次のように表すことができます。\[ \frac{\beta+\gamma}{2} \]先ほど見た、内分する点の表す方を使えば、線分 AD を $2:1$ に内分する点は
\begin{eqnarray} & & \frac{1\cdot\alpha+2\cdot\frac{\beta+\gamma}{2} }{2+1} \\[5pt] &=& \frac{\alpha+\beta+\gamma}{3} \\[5pt] \end{eqnarray}となります。足して3で割るだけ、というシンプルな式になります。

座標平面上でも、【標準】中点の座標や【標準】三角形の重心の座標で同じような結果が得られることを見ています。複素数平面だと、1つの点を1つの文字で表されるので、少しスッキリしますね。

おわりに

ここでは、複素数平面で、内分点・外分点や、中点・重心を表す方法を見てきました。実部と虚部で分けて考えているので、座標平面上で考えたときと似ている式が得られました。座標平面での内容がわかっていれば、受け入れやすい内容でしょう。