【応用】複素数平面と反転

🕒 2019/02/23 🔄 2023/05/01

ここでは、複素数平面上で、鏡映の反転によって図形がどのように移動するかを見ていきます。

📘 目次

複素数平面と反転その１

例題1

複素数平面上で点 $\mathrm{ P }(z)$ が次の等式を満たしているとき、複素数 $w=\dfrac{1}{z}$ に対応する点 $\mathrm{ Q }(w)$ はどのような図形を描くか、答えなさい。
(1) $|z-2|=1$
(2) $|z-1|=1$

どちらも、点 P は円周上の点ですね。中心が違うだけです。これが、 $w=\dfrac{1}{z}$ によってどういう図形に移るか考えてみましょう。

この変換式を変形すると $z=\dfrac{1}{w}$ となります。なお、 $z,w\ne 0$ であることに注意します。これを(1)の式に代入すれば
\begin{eqnarray} \left|\frac{1}{w}-2\right| &=& 1 \\[5pt] |1-2w| &=& |w| \\[5pt] 2\left|w-\frac{1}{2}\right| &=& |w| \\[5pt] \end{eqnarray}となります。この式は、原点を O とし、点 $\dfrac{1}{2}$ を点 A とすると、 $\mathrm{ AQ:QO }=1:2$ であることを表しています。これは、【基本】複素数平面と円で見た通り、アポロニウスの円を表すことになります。

このことから、先ほどの式は、線分 AO を $1:2$ に内分する点、外分する点を直径とする円を表します。つまり、点 $\dfrac{1}{3}$ と点 $1$ を結んだ線分を直径とする円なので、点 Q は、点 $\dfrac{1}{2}$ を中心とする半径 $\dfrac{1}{3}$ の円の上を動くことがわかります。除く点はありません。

試験では、上のリンク先でやっているように、計算によって求めるのが普通ですが。

同じように、 $z=\dfrac{1}{w}$ を(2)の式に代入すれば
\begin{eqnarray} \left|\frac{1}{w}-1\right| &=& 1 \\[5pt] |1-w| &=& |w| \\[5pt] |w-1| &=& |w| \\[5pt] \end{eqnarray}となります。これは、原点 O からの距離と点 $1$ からの距離が等しいことを表すため、点 Q は、原点 O と点 $1$ を結ぶ線分の垂直二等分線となります。

$w=\dfrac{1}{z}$ という変換を「鏡映の反転」といいます。鏡映の反転によって、一般的に次のように変換されます。

原点を通らない円　⇒　原点を通らない円
原点を通る円　⇒　原点を通らない直線

1つ目の例が例題の(1)に、2つ目の例が例題の(2)に対応しています。

一般に、中心 O 、半径 $r$ の円と点 P があったときに、半直線 OP 上に、 $\mathrm{ OP\cdot OQ }=r^2$ となる点 Q をとって、点 P に点 Q を対応させることを、反転といいます。また、線対称になるよう、鏡のように移動することを鏡映と言います。\[ z=r(\cos\theta+i\sin\theta) \]に対して、 $w=\dfrac{1}{z}$ を対応させることは、\[ \dfrac{1}{r}\{\cos(-\theta)+i(-\sin\theta)\} \]を対応させることであり、鏡映と反転を同時に行った変換だと考えることができます。そのため、この変換は「鏡映の反転」と呼ばれているわけなんですね。

ちなみに、(1)で、点同士の対応は、次の図のようになります。

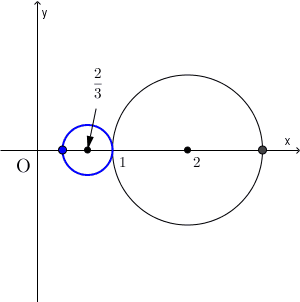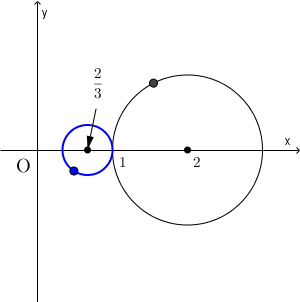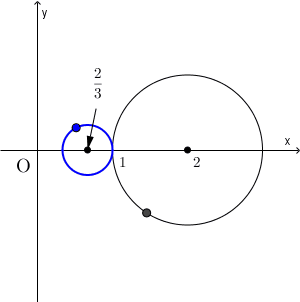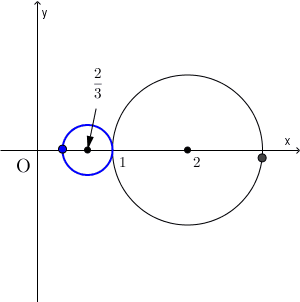
複素数平面と反転その２

例題2

複素数平面上で点 $\mathrm{ P }(z)$ が次の等式を満たしているとき、複素数 $w=\dfrac{1}{z}$ に対応する点 $\mathrm{ Q }(w)$ はどのような図形を描くか、答えなさい。
(1) $|z-1|=|z+1|$
(2) $|z-1|=|z|$

今度は、どちらも直線です。(1)は、虚軸、(2)は原点と点 $1$ とを結んだ線分の垂直二等分線ですね。

先ほどと同じように、 $z=\dfrac{1}{w}$ を使いましょう。なお、 $z,w\ne 0$ であることに注意します。この式を(1)の式に代入すれば
\begin{eqnarray} \left|\frac{1}{w}-1\right| &=& \left|\frac{1}{w}+1\right| \\[5pt] |1-w| &=& |1+w| \\[5pt] |w-1| &=& |w+1| \\[5pt] \end{eqnarray}となります。つまり、変換後も、虚軸であることがわかります。ただ、原点だけは除きます。

次に、(2)について見てみましょう。
\begin{eqnarray} \left|\frac{1}{w}-1\right| &=& \left|\frac{1}{w}\right| \\[5pt] \left|1-w\right| &=& 1 \\[5pt] |w-1| &=& 1 \\[5pt] \end{eqnarray}となります。よって、点 Q が描く図形は、「点 $1$ を中心とする半径 $1$ の円、ただし、原点を除く」となります。

一般に、鏡映の反転によって、直線は、次のように変換されます。

原点を通る直線　⇒　原点を通る直線から原点を除いた図形
原点を通らない直線　⇒　原点を通る円から原点を除いた図形

1つ目の例が例題の(1)に、2つ目の例が例題の(2)に対応しています。

さて、最後に少し小さな疑問について考えておきましょう。気にならない人は、以下の文は流し読みでも構いません。

例題1(2)で見たように、原点を通る円は、原点を通らない直線に移ります。しかし、例題2(2)で見たように、原点を通らない直線は、原点を通る円全体ではなく、円から原点を除きました。2回戻ると元に戻りそうな気がしますが、一番初めにあった「原点」に対応する点はどこにいっちゃったのでしょう。

よく考えてみると、もともと、円から直線へ移したときには、原点に対応する点は直線にはないんですね（直線のずっと遠くの点に対応していると考えることもできますが）。円周上にあった原点に対応する点が直線上にはないので、もう一度変換しても、やはり円周上にあった原点に対応する点はありません。原点に対応する点がどこかにいってしまったのではなく、そもそも対応していなかったんですね。