【基本】複素数平面と円
ここでは、複素数平面上で、円をどのように表すかを見ていきます。
複素数平面と絶対値の復習
【基本】複素数平面と絶対値で見たように、絶対値とは、原点との距離を表します。 $|1+i|$ であれば、点 $1+i$ と原点との距離、つまり、 $\sqrt{1^2+1^2}=\sqrt{2}$ を表すということです。
実部と虚部を使って絶対値を表すこともできますが、共役複素数を用いた\[ |\alpha|^2=\alpha\overline{\alpha} \]という表し方もよく使われます。
また、原点との距離ではなく、2点間の距離であれば、差の絶対値で表すことができます。点 $\mathrm{A}(\alpha)$ と点 $\mathrm{B}(\beta)$ との距離であれば、 $|\beta-\alpha|$ で表すことができます。
これらを利用すると、複素数平面上での円を、等式で表すことができるようになります。
複素数平面と円
複素数平面で、点 $\alpha$ を中心とした半径 $r$ の円について考えてみましょう。 $r$ は正の実数とします。
この円上の点を $z$ とすると、中心との距離が $r$ ということなので、さきほどの絶対値を用いて\[ |z-\alpha|=r \]が成り立つことがわかります。逆に、これを満たす $z$ は円上の点でもあることから、この式が円の方程式であることがわかります。
例えば、 $|z|=3$ であれば、原点を中心とした半径 $3$ の円です。 $|z-i|=1$ であれば、点 $i$ を中心とした半径 $1$ の円です。 $|z+1+i|=2$ なら、点 $-1-i$ を中心とした半径 $2$ の円となります。
距離の比と軌跡
円の方程式を用いて、次の問題を考えてみましょう。【基本】軌跡(距離の比と円)で見た内容を、複素数平面に置き換えたものです。
点 P に対応する複素数を $z$ と置きましょう。OP の長さは $|z|$ です。また、 AP の長さは $|z-3|$ です。よって、 $z$ が満たす条件式は\[ 2|z-3|=|z| \]となります。
このままでは、 $z$ がどのような図形上を動くのかわからないので、この式を変形していきましょう。両辺とも正なので2乗して変形していくと
\begin{eqnarray}
2^2|z-3|^2 &=& |z|^2 \\[5pt]
4(z-3)(\overline{z-3}) &=& z\overline{z} \\[5pt]
4(z-3)(\overline{z}-3) &=& z\overline{z} \\[5pt]
4z\overline{z}-12z-12\overline{z}+36 &=& z\overline{z} \\[5pt]
3z\overline{z}-12z-12\overline{z}+36 &=& 0 \\[5pt]
z\overline{z}-4z-4\overline{z}+12 &=& 0 \\[5pt]
\end{eqnarray}となります。ここで、 $-4z-4\overline{z}$ の部分がうまく積で表現できるように変形していきます。
\begin{eqnarray}
z\overline{z}-4z-4\overline{z}+12 &=& 0 \\[5pt]
(z-4)(\overline{z}-4)-16+12 &=& 0 \\[5pt]
(z-4)(\overline{z-4}) &=& 4 \\[5pt]
|z-4|^2 &=& 2^2 \\[5pt]
|z-4| &=& 2 \\[5pt]
\end{eqnarray}となります。この式から、軌跡は、点 $4$ を中心とする半径 $2$ の円であることがわかります。
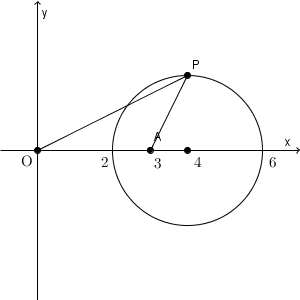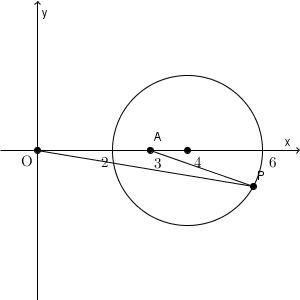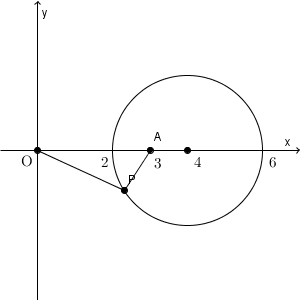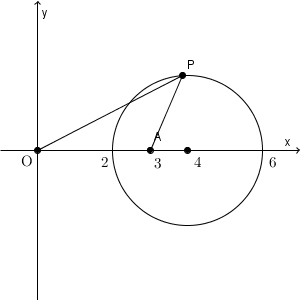
ここでは、かなり丁寧に計算していますが、慣れてくればもっと端折ってもいいでしょう。ほとんど同じ計算ですが、【基本】軌跡(距離の比と円)で行った変形よりも、複素数平面で考えたほうがすっきり書けると思います。
アポロニウスの円と垂直二等分線
【基本】軌跡(距離の比と円)でも書いていますが、 $m$ を $1$ 以外の正の実数とするとき、2点からの距離の比が $1:m$ である点全体の集合は、円になります。この円を、アポロニウスの円といいます。
$1:1$ のときは、垂直二等分線になります。つまり、2点 $\mathrm{A}(\alpha)$, $\mathrm{B}(\beta)$ に対して、線分 AB の垂直二等分線を表す方程式は\[ |z-\alpha|=|z-\beta| \]となります。
おわりに
ここでは、複素数平面上で、円がどのように表されるかを見ました。また、円であることを示すためによく使われる式変形も見てきました。 $|\alpha|^2=\alpha\overline{\alpha}$ を使う変形に慣れるようにしましょう。





