【基本】複素数平面と絶対値

🕒 2019/01/30 🔄 2023/06/14

ここでは、複素数の絶対値について見ていきます。なお、 a, b は実数とします。

📘 目次

絶対値

実数の世界で、絶対値というものを扱いました。
\begin{eqnarray} | a | = \begin{cases} a & ( a \geqq 0 ) \\ -a & ( a \lt 0 ) \end{cases} \end{eqnarray}「0以上のときはそのまま、マイナスのときはマイナスを掛けてプラスにする」というものです。また、これは、数直線上で考えれば、「原点からの距離を表している」と解釈することもできるのでした。（参考：【基本】絶対値）

複素数の場合は、正や負という概念はありません。しかし、「原点からの距離」は考えることができます。これを利用して、複素数の絶対値を考えます。

$\alpha=a+bi$ としましょう。

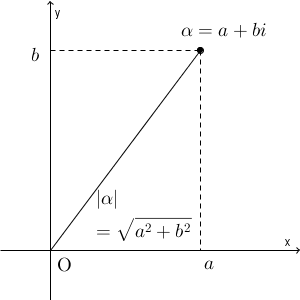
このとき、原点と点 $\alpha$ との距離は、 $\sqrt{a^2+b^2}$ で表すことができます。これを、複素数 $\alpha$ の絶対値(absolute value) といい、 $|\alpha|$ や、 $|a+bi|$ と表します。

複素数の絶対値

$\alpha=a+bi$ のとき、$\sqrt{a^2+b^2}$ を $\alpha$ の絶対値といい、 $|\alpha|$ で表す。

例えば、 $|4-3i|=\sqrt{4^2+(-3)^2}=5$ などと計算できます。

実部・虚部をそれぞれ2乗して足すため、 $|-\alpha|$ や $|\overline{\alpha}|$ も $|\alpha|$ と同じになることがわかります。また、これらが同じであることは、絶対値が原点からの距離を表していることからも理解できます。

もし、 $\alpha$ が実数のとき、つまり、 $b=0$ のときは、 $|\alpha|=\sqrt{a^2}$ となりますが、この右辺は、実数 $a$ の絶対値と一致します。なので、この定義は、実数の絶対値の定義を拡張したもの、と考えることができます。

絶対値と共役複素数の関係

$\alpha=a+bi$ のときは、 $|\alpha|=\sqrt{a^2+b^2}$ と書くことができますが、実部と虚部を使わずに絶対値を表すこともできます。このような表現が役立つ場面も今後出てきます。

$\alpha\overline{\alpha}$ を計算してみると、次のことがわかります。
\begin{eqnarray} (a+bi)\overline{(a+bi)} &=& (a+bi)(a-bi) \\[5pt] &=& a^2+b^2 \\[5pt] &=& |\alpha|^2 \\[5pt] \end{eqnarray}よって、 $|\alpha|^2=\alpha\overline{\alpha}$ が成り立ちます。 $|\alpha|=\sqrt{\alpha\overline{\alpha} }$ という形で使われることもあります。

実数のときには、 $|a|^2=a^2$ としましたが、複素数のときは、 $|\alpha|^2=\alpha\overline{\alpha}$ となることに注意しましょう。

複素数平面上での2点間の距離

絶対値が原点からの距離であることを見ましたが、2点間の距離を表すのにも絶対値が使えます。

$\mathrm{ A }(\alpha)$, $\mathrm{ B }(\beta)$ とし、この2点間の距離について考えましょう。

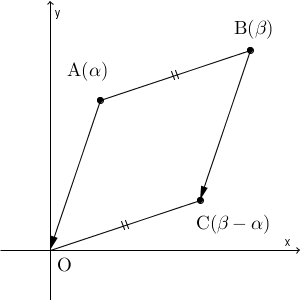
この点A が原点に来るように平行移動すると、点B は、点 $(\beta-\alpha)$ に移動することになります。この点を C とすると、 AB と OC の長さは等しく、 OC の長さは $|\beta-\alpha|$ で表すことができるので、2点 $\alpha$, $\beta$ 間の距離は、 $|\beta-\alpha|$ とかけることがわかります。