【基本】複素数平面と複素数の加法・減法・実数倍

ここでは、複素数の加法・減法を、複素数平面上で考えてみます。なお、a, b, c, d は実数とします。

複素数の加法・減法

$\alpha=a+bi$, $\beta=c+di$ とし、これらを表す点を A, B とします。

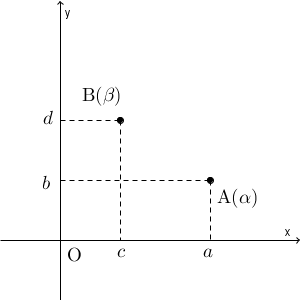
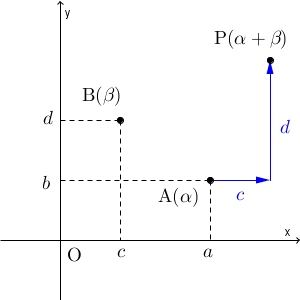
このとき、和は\[ \alpha+\beta=(a+c)+(b+d)i \]となります。これは、複素数平面上では、点 A を、実軸方向に $c$ だけ移動し、虚軸方向に $d$ だけ移動して移る点、と考えることができます。この点を P とすると、図は次のようになります。

一方、差は、\[ \alpha-\beta=(a-c)+(b-d)i \]となります。これを図で考えると、点 A を、実軸方向に $-c$ だけ移動し、虚軸方向に $-d$ だけ移動して移る点、と考えることができます。この点を Q とすると、図は次のようになります。

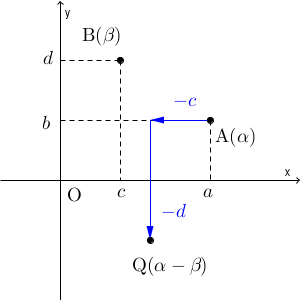
つまり、複素数の加法・減法は、複素数平面上では、平行移動を表していると考えることができます。

また、次のように、平行四辺形を使って考えることもできます。O, A, B が一直線上にないときは、 $\alpha+\beta$ に対応する点は、 O が B に移るように、点 A を平行移動して移る点だから、線分 OA, OB を2辺とする平行四辺形の第4の頂点であることがわかります。

$-\beta$ を表す点を C とすると、差の場合、 $\alpha-\beta$ は、線分 OA, OC を2辺とする平行四辺形の第4の頂点であることがわかります。

これらの考え方は、ベクトルのときの考え方に似ていますね。【基本】ベクトルの足し算でも見た通り、 $\overrightarrow{ \mathrm{ OA } }+\overrightarrow{ \mathrm{ OB } }$ を $\overrightarrow{ \mathrm{ OP } }$ とすると、点 $\overrightarrow{ \mathrm{ P } }$ は、四角形 OAPB が平行四辺形となるような点になるのでした。平行四辺形を使って考えられる点は、共通しています。

複素数の実数倍

$\alpha=a+bi$ として、実数 k を掛けたときにどうなるかを考えてみましょう。 $\alpha=0$ のときは何を掛けても $0$ なので、以下では、 $\alpha\ne 0$ として考えます。

$\alpha$ に $k$ を掛けると、 $k\alpha=ka+kbi$ となります。 $\mathrm{ A }(\alpha)$, $\mathrm{ B }(k\alpha)$ とすると、図は次のようになります。

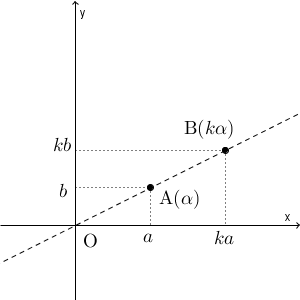
点A と点B とでは、実部と虚部との比が同じなので、点 B は、直線 OA 上にあることがわかります。これは、 $a$ や $b$ が $0$ のときでも成り立ちます。

マイナスの実数を掛けたときは、実部も虚部も符号が変わるので、この場合は、次のような位置関係になります。

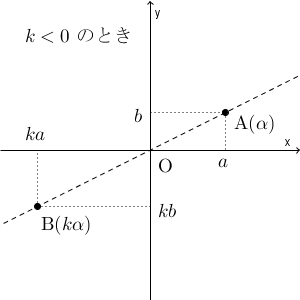
以上から、 $k\gt 0$ ならば、点 B は、原点から見て、点 A と同じ側、 $k\lt 0$ ならば、反対側となることがわかります。 $k=0$ なら、点 B は、もちろん、原点です。

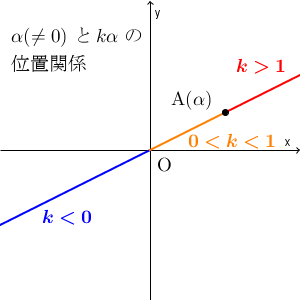
また、 $k\gt 1$ なら、点 B は、原点から見て、点 A より遠いところにあり、 $0\lt k\lt 1$ ならば、線分 OA 上にあります。 $k=1$ のときは、もちろん、点 A と点 B は一致しています。

つまり、複素数の実数倍は、複素数平面上では、原点を中心とした、拡大・縮小を表していると考えられます。

この場合も、ベクトルの計算と対応しています。 $\overrightarrow{ \mathrm{ OB } }=k\overrightarrow{ \mathrm{ OA } }$ としたとき、点 O, A, B の位置関係は、上で見た図と同じになります。（参考：【基本】ベクトルの定数倍）

おわりに

ここでは、複素数の加法・減法・実数倍が、複素数平面上でどういうことを表しているかを見てきました。加法・減法は平行移動、実数倍は拡大・縮小を表しているのでした。実部・虚部がどう変化するかを考えれば、簡単に確かめることはできますが、複素数平面上でどのように対応しているのか、パッとわかるようになっておきましょう。