【基本】複素数平面の導入
ここでは、複素数平面を導入し、複素数平面を使うことで何ができそうになるのか、を見ていきます。
複素数平面
実数の世界では、数を図示化するために、数直線を使いました。ここでは、複素数を図示化することを考えましょう。
複素数は、2つの実数 $a,b$ を使って、 $a+bi$ と表すことができるのでしたね。2つの実数を使うことから、複素数を図で表すには、平面が必要だと考えられます。
これを踏まえ、複素数 $\alpha=a+bi$ に対して、次のように、点 $(a,b)$ を対応させることにしましょう。
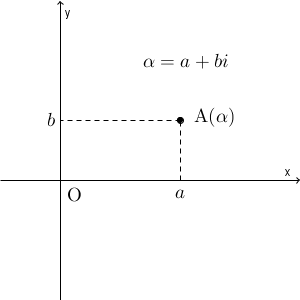
こうすると、複素数と座標平面上の点は、1つずつもれなくダブりなく対応します。このように、複素数を座標平面上の点で表したとき、この平面のことを、複素数平面(complex plane) といいます。複素平面と呼ぶこともあります。
複素数平面上では、 $x$ 軸のことを実軸、 $y$ 軸を虚軸といいます。実軸上の点は実数を表しています。虚軸上の点のうち、原点以外の点は、純虚数を表します。
複素数平面上での点の表し方はいくつかあります。 $\alpha=a+bi$ に対応する点を A とすると、 $\mathrm{ A }(\alpha)$ や $\mathrm{ A }(a+bi)$ と書きます。これで、点 A と複素数 $\alpha=a+bi$ とが対応していることを表します。もっと簡単に、この点 A のことを、点 $\alpha$ と書くこともあります。
実軸は、実数に対応するので、複素数平面は数直線を拡張したもの、と考えることができます。
複素数平面で具体的な点を考えてみよう
具体的に、複素数平面上の点について考えてみましょう。
点 $\mathrm{ P }(3+2i)$, $\mathrm{ Q }(-1)$, $\mathrm{ R }(-2i)$ を複素数平面を使って表すと、次のようになります。
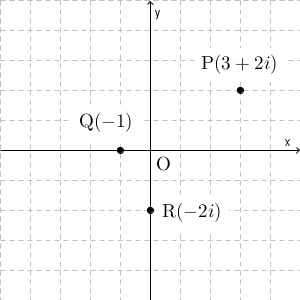
点 P であれば、 $(3,2)$ の点に対応する、ということですね。点 Q は実軸上の点で、点 R は虚軸上の点となります。
さて、ここからは、 $i$ を掛けると、どのような点に移動するかを見てみることにしましょう。
$1+2i$ という複素数について考えてみましょう。これに $i$ を掛けると、次のようになります。\[ (1+2i)i=-2+i \]もう一度かけると、\[ (-2+i)i=-1-2i \]となります。さらにもう一度かけると\[ (-1-2i)i=2-i \]となり、最後にもう一度かけると\[ (2-i)i=1+2i \]となります。最後の値は最初と同じ結果であり、元に戻っていますね。
はじめの複素数に対応する点を A として、 $i$ を掛けた結果に対応する点を順番に B, C, D と置くことにしましょう。つまり、 $\mathrm{ A }(1+2i)$, $\mathrm{ B }(-2+i)$, $\mathrm{ C }(-1-2i)$, $\mathrm{ D }(2-i)$ とする、ということです。これらの点は、複素数平面上では次のようになります。
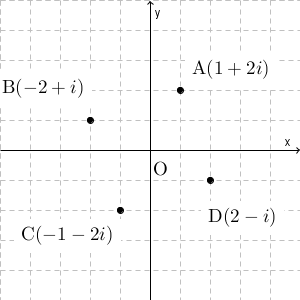
この段階で気づく人もいるかもしれませんが、もっとわかりやすくするために、円や線を追加してみましょう。
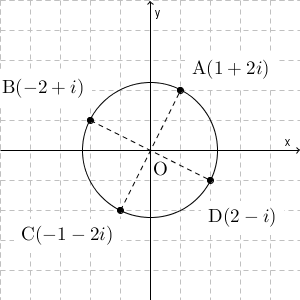
この図からもわかりますが、 A, B, C, D は、原点を中心として反時計回りに90度ずつ回転していることがわかります。つまり、複素数の世界で $i$ を掛けることと、複素数平面の世界で90度ずつ回転することが対応している、と考えられるわけですね。
この考え方は、今後の内容を学んでいくと、正しいことがわかります。このため、複素数の掛け算を使って点の回転を考える、といったことができるようになります。これらのことを学んでいくと、複素数や複素数平面を考えるメリットが体感できるようになっていきます。
おわりに
ここでは、複素数を平面上の点で表す複素数平面について見てきました。また、後半では、複素数の掛け算が、複素数平面上での回転に対応してそうだ、ということを見ました。実際にどのように対応しているかは、別の機会に見ていくことになります。





