【基本】複素数平面と共役複素数

ここでは、共役複素数を、複素数平面上で考えてみます。なお、 a, b, c, d は実数とします。

共役複素数

$\alpha=a+bi$ に対して、共役複素数 $\overline{\alpha}$ は $a-bi$ のことを言うのでした。これを複素数平面上で考えてみましょう。点 $\alpha$, $\overline{\alpha}$ をかいてみます。

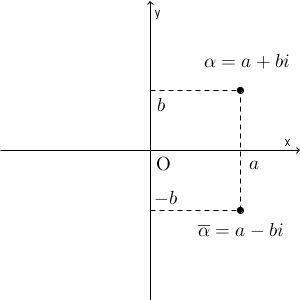
このように、共役複素数は虚部の符号を変えたものなので、実軸について対称な点を表していることがわかります。

対称移動という観点で、 $-\alpha$ についても見てみましょう。

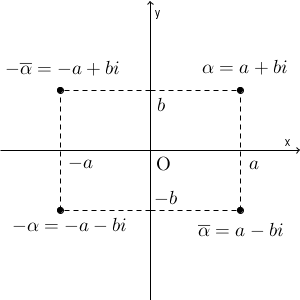
$-\alpha$ は、原点について対称な点を表しています。また、虚軸について対称な点は、これら2つを組み合わせて、 $-\overline{\alpha}$ で表すことができます。

共役複素数は、複素数平面上では、実軸に関する対称移動に対応していることがわかります。

共役複素数を用いて実部と虚部を表す

今まで、実部と虚部を使って複素数を表してきましたが、共役複素数を使えば、逆に、実部と虚部を表すことができます。

$\alpha=a+bi$ とすると、 $\alpha+\overline{\alpha}=2a$ となるので、\[ a=\frac{\alpha+\overline{\alpha} }{2} \]と表すことができます。また、 $\alpha-\overline{\alpha}=2bi$ となるので、\[ b=\frac{\alpha-\overline{\alpha} }{2i} \]と表せます。

複素数から、実部だけ、虚部だけを抜き出したいときに、このような変形を使うことがあります。

共役複素数を用いて実数であるための条件を考える

ここでも、 $\alpha=a+bi$ とします。

虚部が $0$ のとき、つまり、 $b=0$ のときは、複素数は実数を表すことになります。 $b=\dfrac{\alpha-\overline{\alpha} }{2i}$ だったので、 $\alpha$ が実数であることは、 $\overline{\alpha}=\alpha$ が成り立つことと同値です。これは、複素数が実数であることを証明するために、よく使われます。

このことを、複素数平面上で考えてみましょう。点 $\overline{\alpha}$ は、点 $\alpha$ を実軸について対称移動したものなので、 $\overline{\alpha}=\alpha$ は、「実軸について対称移動しても変わらない」ことを表しています。このことからも、これが $\alpha$ が実数であることと同値であることがわかります。

実部が $0$ であり、虚部が $0$ 以外のときは、純虚数というのでした。これは、 $a=0$, $b\ne 0$ のことなので、 $\alpha$ が純虚数であることは、 $\overline{\alpha}=-\alpha$, $\alpha\ne 0$ が成り立つことと同値です。

共役複素数と四則演算の性質

最後に、共役複素数と四則演算についての、基本的な性質を紹介します。

例えば、一つ目は、足してから共役複素数を考えても、共役複素数を足しても、結果は変わらない、ということです。四則演算を行うのと共役複素数を考える順番は、交換することができる、ということです。

これらは、具体的に計算することで示せます。 $\alpha=a+bi$, $\beta=c+di$ とすると、一つ目は
\begin{eqnarray} \overline{\alpha+\beta} &=& \overline{(a+c)+(b+d)i} \\[5pt] &=& (a+c)-(b+d)i \\[5pt] &=& (a-bi)+(c-di) \\[5pt] &=& \overline{\alpha}+\overline{\beta} \\[5pt] \end{eqnarray}と示せます。

平行移動してから実軸について反転するのと、実軸について反転してから上下反対に平行移動したものは同じ、というのは、複素数平面上で考えても成り立つことが理解できるでしょう。

積や商は、少し計算が大変ですが、両辺をそれぞれ計算することで示すことができます。単純に計算するだけですが、少し複雑なので【標準】共役複素数の性質（積や商）で見ることにしましょう。

おわりに

ここでは、共役複素数を複素数平面上で考えてみました。共役複素数を考えることは、実軸に関する対称移動に対応しているのでした。また、実部や虚部を抜き出す方法や、共役複素数を用いて実数であるための条件を表す方法も見ました。これらは、よく使われるので覚えておきましょう。