【基本】絶対値
ここでは、数の"大きさ"を表す「絶対値」について見ていきます。また、絶対値の説明の前に、数直線についても触れます。
数直線
一般的に、説明するときには、「文字」を使うよりも「図」を使って説明したほうが都合がいいことが多いです。数の大小や順序を説明するときも同様で、「図」を使った方が説明しやすいことが多いんですね。そこで使われるのが、「数直線」です。
「数直線」と特別な名前はついていますが、そんなに難しいものではありません。下のようなものです。
基準となる「0」があります。これを「原点」と呼び、O で表します。この直線上の1つ1つの点が、1つ1つの数に対応している、と考えます。
右側に行くほど大きい数、左に行くほど小さい数を表します。「右のほうが大きい」ことを示すために、右端に矢印「→」を書きます。$b$ の方が大きいなら、b を表す点が右側にきます($b$ の方が大きいことを、「$a\lt b$」と書きます。)。
また、数直線上の点 A に対応する数が a のとき、$\mathrm{A}(a)$ と書きます。
どのような目盛りを入れるかは場合によって異なりますが、自分でかくときは、「数」と「数直線上での位置関係」が対応するようにします。
絶対値
数を扱うときに、「数そのもの」ではなく「数の大きさ」に着目したい場合があります。
例えば、AさんとBさんの2人がゲームをするとし、それぞれの得点を $a$ 点、$b$ 点とします。この2人の点差が10点になったら、ゲームが終了するとしましょう。このゲーム終了の条件を数式で書くと、どうなるでしょうか。
普通に書けば、「$a-b=10$ または $a-b=-10$」となります。しかし、ゲームが終了するのに重要なのは、「$a-b$ の答え」というよりは、「答えの大きさ」なんですよね。つまり、符号は必要ありません。「符号をとった数字が、10かどうか」が条件なんですね。
このように、数の大きさに着目したいときに、絶対値を使うと便利です。
実数の絶対値(absolute value) は、「0以上のときはそのまま、マイナスのときはマイナスを掛けてプラスにしたもの」と定義されます。絶対値は必ず0以上の値になります。
式で書くと、次のようになります。左辺の $|x|$ は、「x の絶対値」を表す記号です。
\begin{eqnarray}
| x |
=
\begin{cases}
x & ( x \geqq 0 ) \\
-x & ( x \lt 0 )
\end{cases}
\end{eqnarray}
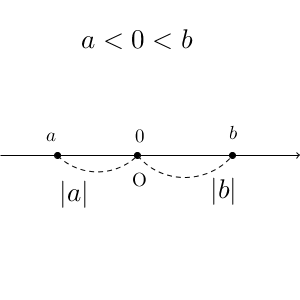
数直線でいうと、絶対値は「原点からの距離」にあたります。次の図は、距離が絶対値にあたることを、「0より小さい $a$」と「0より大きい $b$」に対して示したものです。
絶対値の計算
絶対値の計算は、絶対値の中身の符号によって変わります。下に3つの例を挙げています。
\begin{eqnarray}
|3| &=& 3 \\[5pt]
|-3| &=& 3 \\[5pt]
\left|-\frac{1}{3} \right| &=& \frac{1}{3} \\
\end{eqnarray}これらは、絶対値の中身が正か負かすぐわかりますね。結果的には、マイナスがある場合は、マイナスをとるだけです。
絶対値が複数ある場合は、内側から順番に計算していきます。
\begin{eqnarray}
\Big| |-1| - |-3| \Big|
&=&
| 1-3 | \\
&=&
| -2 | \\
&=&
2
\end{eqnarray}
$|-2|$ のようにシンプルな場合は、マイナスをとるだけで絶対値の値がわかりますが、「マイナスをとるだけ」ではダメなときもあります。あくまでも「マイナスの場合は、全体にマイナスを掛ける」と計算するのが、本来の計算方法です。
\begin{eqnarray}
& &
|-1-\sqrt{2}| + |1-\sqrt{2}| \\
&=&
-(-1-\sqrt{2}) -(1-\sqrt{2}) \\
&=&
1+\sqrt{2} -1+\sqrt{2} \\
&=&
2\sqrt{2} \\
\end{eqnarray}$|1-\sqrt{2}|$ の場合、この値は $\sqrt{2}-1$ であり、「マイナスをとるだけ」では正しくないことがわかりますね。
最後の計算からもわかる通り、絶対値がついている計算でやっかいなのは、「絶対値の中身が正か負かわかりにくいとき」なんですね。$1-\sqrt{2}$ が正か負かは、それまでに出てきた例に比べるとわかりづらいです。
今後は、絶対値の中に文字が含まれるケースも出てきます。そうすると、絶対値の中身が正か負か決まらない場合もあります。そのときは場合分けが必要になってくるため、この記事で紹介したよりも難易度が高くなります。





