【応用】複素数平面と垂心
ここでは、複素数平面上で、垂線や垂心について見ていきます。
複素数平面と垂線
複素数平面上において、単位円周上に異なる3点 $\mathrm{A}(\alpha)$, $\mathrm{B}(\beta)$, $\mathrm{C}(\gamma)$ をとるとします。このとき、三角形 ABC の垂心がどのように表されるかを考えていきましょう。

垂心とは、【標準】三角形の垂心(なぜ3つの垂線は1点で交わるか)でも見た通り、各頂点から対辺へ下した垂線の交点です。3つの垂線は一点で交わるので、それを垂心と呼ぶのでした。
なので、垂心を考えるためには、まず、垂線について考えていくのがいいでしょう。
対称性があるのでどこから考えてもいいのですが、点 A から辺 BC に下した垂線について考えてみましょう。
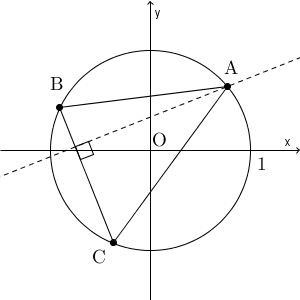
この垂線上の点を $\mathrm{ P }(z)$ とおくと、 $\mathrm{ P\ne A }$ のときは、 AP と BC は垂直に交わります。このことを複素数を用いて表してみましょう。
【標準】複素数平面と同一直線上にある3点では、直線 AB, AC が垂直に交わるときを扱いましたが、これと似た発想で考えることができます。点 A が原点にくるように線分 AP を平行移動し、点 B が原点に来るように線分 BC を平行移動したとしましょう。
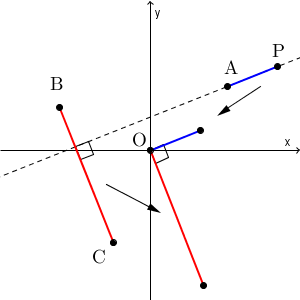
このように平行移動しても、平行移動する前に垂直だったなら、平行移動した後同士の線分も垂直に交わります。そのため、\[ \frac{z-\alpha}{\gamma-\beta} \]は、 $0$ または純虚数となります。これを共役複素数を用いて表せば、次のようになります。\[ \frac{z-\alpha}{\gamma-\beta} = -\overline{ \left(\frac{z-\alpha}{\gamma-\beta}\right) } \]点 $\mathrm{ P }(z)$ が垂線上にあればこの式を満たすし、この式を満たすものはすべて垂線上にあるので、これは、 点 A から辺 BC に下した垂線を表す式となります。単位円上にあることを使ってないので、これは一般的に成り立つ式です。
この式を変形してみましょう。分母を払って変形すると
\begin{eqnarray}
(z-\alpha)(\overline{\gamma}-\overline{\beta} ) = -(\gamma-\beta)(\overline{z}-\overline{\alpha})
\end{eqnarray}となります。ここで、 A, B, C は、単位円周上の点なので、\[ \alpha\overline{\alpha}=|\alpha|^2=1 \]などの式が成り立つので、共役複素数の部分を変形して
\begin{eqnarray}
(z-\alpha)\left(\frac{1}{\gamma}-\frac{1}{\beta}\right) &=& -(\gamma-\beta)\left(\overline{z}-\frac{1}{\alpha}\right) \\[5pt]
(z-\alpha)\cdot \frac{\beta-\gamma}{\beta\gamma} &=& (\beta-\gamma)\left(\overline{z}-\frac{1}{\alpha}\right) \\[5pt]
(z-\alpha)\cdot \frac{1}{\beta\gamma} &=& \overline{z}-\frac{1}{\alpha} \\[5pt]
\alpha z-\alpha^2 &=& \alpha\beta\gamma\overline{z}-\beta\gamma \\[5pt]
\end{eqnarray}となります。
複素数平面と垂心
点 A から辺 BC に下した垂線がこのように表せることを利用して、次に、点 B から辺 AC に下した垂線も表してみましょう。これは、先ほどの式の $\alpha$, $\beta$, $\gamma$ を順番に入れ替えたものとなるので\[ \beta z-\beta^2 = \beta\gamma\alpha\overline{z}-\gamma\alpha \]となります。この2つを同時に満たす $z$ が垂心ですね。ここで、2つの式の $\overline{z}$ の前の部分が同じなので、辺々引いてみると、うまい具合に $z$ だけが残ります。こうして、次のように計算できます。
\begin{eqnarray}
(\alpha-\beta) z-(\alpha^2-\beta^2) &=& -\beta\gamma+\gamma\alpha \\[5pt]
z-(\alpha+\beta) &=& \gamma \\[5pt]
z &=& \alpha+\beta+\gamma \\[5pt]
\end{eqnarray}おー、すごくきれいな式が出てきましたね。
「単位円周上の3点」というのは重要な条件です。一般的にこのような式で書けるわけではありません。外心が原点ではない場合は、原点にくるように平行移動しておく必要があります。
外心と垂心と重心の関係について
先ほどの垂心の式は、ある式に似ています。【基本】複素数平面と内分点・外分点で見た、重心です。重心は、次のように表すことができます。\[ \frac{\alpha+\beta+\gamma}{3} \]また、ここで見た問題では、原点は外心ですね。
よって、外心 O、重心 G、垂心 Hは、この順番に一直線上にあり、 $\mathrm{ OG:GH }=1:2$ が成り立つことがわかります。このことは、外心が原点ではない場合にも成り立ちます。
おわりに
ここでは、複素数平面上で、単位円周上の3点を結んで作られた三角形の垂心について考えました。また、重心や外心との関係についても見ました。垂直と純虚数の関係、共役複素数との関係をおさえて、式で表現できるようにすると、導けるようになります。





