🏠 Home / 数学C / 複素数平面 / 複素数平面と図形

【標準】複素数平面と連動して動く点

🕒 2019/02/15 🔄 2023/05/01

ここでは、円周上を動く点に連動して動く点が、どのような軌跡を描くか、考えていきます。

📘 目次

円周上を動く点に連動して動く点その１

例題1

複素数平面上で、点A$(z)$ が、原点を中心とする半径 $2$ の円周上を動くとき、点 B($4$) と点 A とを結ぶ線分の中点 P$(w)$ の軌跡を求めなさい。

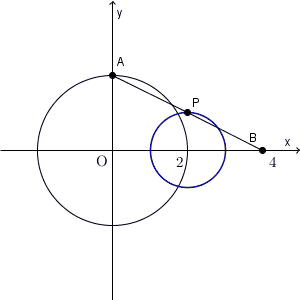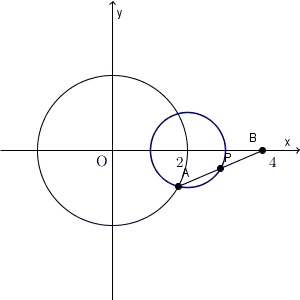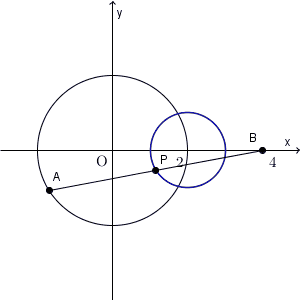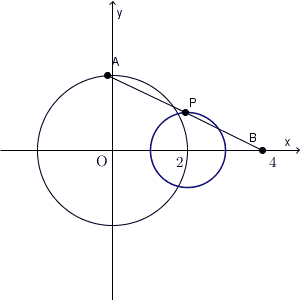
図は、次のようになっています。

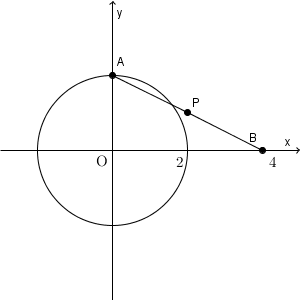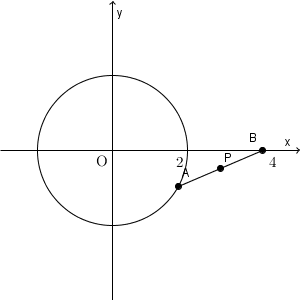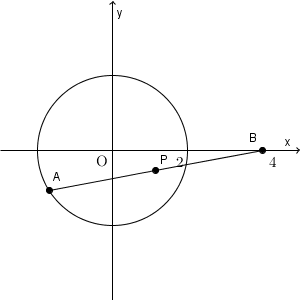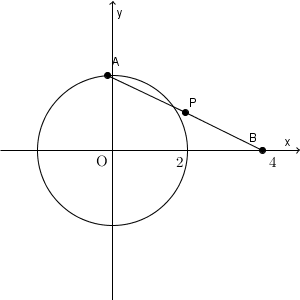
実質的には、【基本】軌跡（連動して動く点）で見た内容と同じ問題です。

「点A$(z)$ が、原点を中心とする半径 $2$ の円周上を動く」とありますが、これを式で表すと次のようになります。\[ |z|=2 \]原点からの距離が $2$ である、という式ですね（参考：【基本】複素数平面と円）。

次に、「点 P$(w)$ は、点 B($4$) と点 A とを結ぶ線分の中点」なので、これを式で表すと\[ \frac{4+z}{2}=w \]となります（参考：【基本】複素数平面と内分点・外分点）。

2つ目の式を変形すると
\begin{eqnarray} 4+z &=& 2w \\[5pt] z &=& 2w-4 \\[5pt] \end{eqnarray}となるので、これを1つ目の式に代入します。半径と中心がわかるように変形すると \begin{eqnarray} |z| &=& 2 \\[5pt] |2w-4| &=& 2 \\[5pt] |w-2| &=& 1 \end{eqnarray}となります。この式は、中心が点 $2$ で、半径が $1$ の円を表しています。これが求める軌跡となります。

また、次のように考えてもいいでしょう。\[ w=\frac{z}{2}+2 \]と変形できるので、複素数平面上では、原点を中心に $\dfrac{1}{2}$ 倍して、実軸方向に $2$ だけ平行移動した変形だと考えることができます。原点を中心に $\dfrac{1}{2}$ 倍すれば、半径 $2$ の円は半径 $1$ の円となり、平行移動することで中心が点 $2$ に移動します。こうして、上と同じ答えを導き出すこともできます。

円周上を動く点に連動して動く点その２

例題2

点 z が、原点を中心とする半径 $2$ の円周上を動くとき、次の式で表される点 w の軌跡を求めなさい。\[ w=iz-i \]

今回は、どのように連動するかが少しわかりづらいですが、先ほどと似たような計算で求めることができます。

先ほどと同様に、 $z$ は $|z|=2$ を満たします。次に、 $w$ の式を変形すると\[ z=\frac{w+i}{i} \]となります。これを $|z|=2$ に代入して整理すると
\begin{eqnarray} \left| \frac{w+i}{i} \right| &=& 2 \\[5pt] \frac{|w+i|}{|i|} &=& 2 \\[5pt] |w-(-i)| &=& 2 \\[5pt] \end{eqnarray}となります。この式は、点 $-i$ を中心とした半径 $2$ の円です。これが求める軌跡となります。

これも、図形的に考えることができます。 $w=iz-i$ のうち、 $iz$ の部分は\[ \left(\cos\frac{\pi}{2} +i\sin\frac{\pi}{2}\right)z \]と書けるので、これは、原点を中心として $\dfrac{\pi}{2}$ だけ回転することを表しています。といっても、今の場合、 $z$ は原点を中心とした円周上を動くので、回転した後も同じ円周上を動きます。さらに、 $-i$ によって、虚軸方向に $-1$ だけ平行移動することがわかります。両者を合わせると、上の軌跡が得られます。

また、このように変形して考えてもいいでしょう。
\begin{eqnarray} w &=& iz-i \\[5pt] &=& i(z-1) \\[5pt] &=& \left(\cos\frac{\pi}{2} +i\sin\frac{\pi}{2}\right)(z-1) \\[5pt] \end{eqnarray}こう考えると、まず $z$ は実軸方向に $-1$ だけ平行移動し、その後で原点を中心に $\dfrac{\pi}{2}$ だけ回転移動することがわかります。このように考えても、同じ結果にたどりつけます。

計算によって考えたり、移動によって考えたりできるので、問題によって、考えやすい方法で解いていくようにしましょう。