【基本】複素数の極形式と積
ここでは、複素数を極形式で表したときに、複素数の積がどのように計算できるかを見ていきます。これを見れば、複素数平面や極形式を考えるメリットがわかってきます。
複素数の極形式と積
0でない2つの複素数 $z_1$, $z_2$ を考えます。これらの極形式を表すと
\begin{eqnarray}
z_1 &=& r_1(\cos\theta_1+i\sin\theta_1) \\[5pt]
z_2 &=& r_2(\cos\theta_2+i\sin\theta_2) \\[5pt]
\end{eqnarray}となるとします。
この極形式を使って、積を計算してみましょう。なんだか $a+bi$ の形で計算するより複雑になっているように見えますが、実はいいことが起こります。
\begin{eqnarray}
& &
z_1z_2 \\[5pt]
&=&
r_1(\cos\theta_1+i\sin\theta_1)\cdot r_2(\cos\theta_2+i\sin\theta_2)\\[5pt]
&=&
r_1r_2(\cos\theta_1\cos\theta_2-\sin\theta_1\sin\theta_2) \\
& & +ir_1r_2(\sin\theta_1\cos\theta_2+\cos\theta_1\sin\theta_2)\\[5pt]
\end{eqnarray}最後の式は、実部と虚部で分けています。ここで、実部を見てみると、カッコの中は、三角関数の加法定理から、 $\cos(\theta_1+\theta_2)$ となることがわかります。また、虚部も、カッコの中は、 $\sin(\theta_1+\theta_2)$ となることがわかります(参考:【基本】正弦・余弦の加法定理の使い方)。つまり、上の計算から
\begin{eqnarray}
& &
z_1z_2 \\[5pt]
&=&
r_1(\cos\theta_1+i\sin\theta_1)\cdot r_2(\cos\theta_2+i\sin\theta_2)\\[5pt]
&=&
r_1r_2\{ \cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2) \}
\end{eqnarray}となることがわかります。
最後の式は極形式になっているので、 $|z_1z_2|=r_1r_2$ と $\arg z_1z_2=\theta_1+\theta_2$ が成り立つことがわかります。絶対値はそのまま掛けるだけ、偏角は、足したものになる、ということですね。
また、 $|z_1z_2|=|z_1||z_2|$ と $\arg z_1z_2=\arg z_1+\arg z_2$ が成り立つ。
例えば、 $2\left( \cos\dfrac{\pi}{6}+i\sin\dfrac{\pi}{6} \right)$ と $3\left( \cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4} \right)$ の積であれば、絶対値同士を掛けて、偏角同士を足して\[ 6\left( \cos\dfrac{5}{12}\pi+i\sin\dfrac{5}{12}\pi \right) \]と計算できます。かなり簡単になりますね。
複素数の積の図形的な意味について
先ほどの積を用いて、複素数の積の図形的な意味を考えてみましょう。
$2\left( \cos\dfrac{\pi}{6}+i\sin\dfrac{\pi}{6} \right)$ と $3\left( \cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4} \right)$ の2点をかいてみます。それぞれ、点 A, B としましょう。
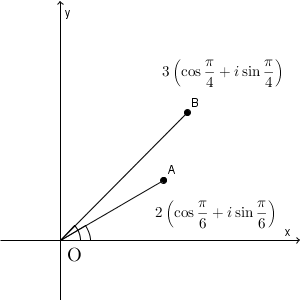
これらを掛けたとき、絶対値は、それぞれの絶対値の積なので、点 B を、原点を中心に $2$ 倍だけ拡大したものと、考えられます。また、偏角は2つの偏角の和となるので、さらに、原点を中心に $\dfrac{\pi}{6}$ だけ回転したものと、考えられます。

このように、複素数を極座標で表したとき、複素数を掛けるということは、絶対値が拡大・縮小を表し、偏角が回転を表していることがわかります。
特に、絶対値が $1$ の複素数、つまり、 $(\cos\theta+i\sin\theta)$ を掛けることは、原点を中心とした回転を表すことになります。【基本】複素数平面の導入では、 $i$ を掛けることと、90度回転することの対応について書きましたが、\[ i=\cos\frac{\pi}{2}+i\sin\frac{\pi}{2} \]と $i$ を極形式の形で書けば、はっきりしますね。
このことから、回転を考えたい場合には、複素数の極形式を用いると便利です。具体的な使い方は、今後見ていくことになります。
おわりに
ここでは、複素数の積が、拡大・縮小と回転を表していることを見ました。特に、偏角が回転を表していることが重要です。このため、図形への応用などで、複素数を使う場面が出てきます。





