【標準】n乗根と極形式
ここでは、ド・モアブルの定理を使って、n 乗根を求める問題を見ていきます。
2乗してiになる数
複素数について学んだときに、2乗して $i$ になる数を求めました(参考:【標準】2乗してiになる複素数)。このときは、 $x+yi$ を2乗した結果と $i$ とを比較して\[ \frac{\sqrt{2} }{2}+\frac{\sqrt{2} }{2}i, \quad -\frac{\sqrt{2} }{2}-\frac{\sqrt{2} }{2}i \]であることを導いていました。
ただ、ド・モアブルの定理を使えば、もう少し簡単に求めることができます。
複素数 $z=r(\cos\theta+i\sin\theta)$ が、 $z^2=i$ を満たすとしましょう。極形式で書くと、左辺は\[ r^2(\cos2\theta+i\sin2\theta) \]であり、右辺の $i$ は、\[ \cos\frac{\pi}{2}+i\sin\frac{\pi}{2} \]となります。絶対値を比較すると $r^2=1$ であり、 $r$ は正の実数なので $r=1$ であることがわかります。
次に偏角を考えます。偏角は $2\pi$ の整数倍だけズレてもいいので、整数 $k$ を用いて、\[ 2\theta=\frac{\pi}{2}+2k\pi \]と書けます。よって、\[ \theta=\frac{\pi}{4}+k\pi \]であり、偏角が $0$ 以上 $2\pi$ 未満となるようにとれば、\[ \theta=\frac{1}{4}\pi,\frac{5}{4}\pi \]となることがわかります。
以上から、2乗して $i$ になるものは、\[ \cos\frac{1}{4}\pi+i\sin\frac{1}{4}\pi, \quad \cos\frac{5}{4}\pi+i\sin\frac{5}{4}\pi \]となり、上で見たものと同じ結果になることがわかります。
図で示すと次のようになります。どちらも、2回回転すると、点 $i$ に移動することがわかります。

このように、ド・モアブルの定理を使えば、簡単に2乗根を計算することができます。また、同じ要領で、3乗根でも4乗根でも計算できます。実部・虚部を比較するやり方では、3乗や4乗だと計算が大変すぎて、答えを出すのが難しくなってしまいます。
n乗根を求める
それでは、2乗根以外の場合を求めてみましょう。 $1$ の $n$ 乗根は【基本】1のn乗根と極形式で求めましたが、 $1$ 以外の場合を見てみます。
$z=r(\cos\theta+i\sin\theta)$ とおいて考えましょう。これを4乗した結果は\[ r^4(\cos 4\theta +i\sin 4\theta) \]です。また、 $8-8\sqrt{3}i$ を極形式で表すと\[ 16 \left(\cos\frac{5}{3}\pi+i\sin\frac{5}{3}\pi\right) \]となります。絶対値を比較すると、 $r^4=16$ となります。 $r$ は正の実数なので、 $r=2$ となります。
偏角は、整数 $k$ を用いて\[ 4\theta=\frac{5}{3}\pi+2k\pi \]なので、\[ \theta=\frac{5}{12}\pi+\frac{k}{2}\pi \]となることがわかります。同じ複素数になるものを除けば、 $k=0,1,2,3$ とすればいいですね。
こうして、 $8-8\sqrt{3}i$ の4乗根は、次の4つであることがわかります。
\begin{eqnarray}
& & 2 \left(\cos\frac{5}{12}\pi+i\sin\frac{5}{12}\pi\right) , \\[5pt]
& & 2 \left(\cos\frac{11}{12}\pi+i\sin\frac{11}{12}\pi\right) , \\[5pt]
& & 2 \left(\cos\frac{17}{12}\pi+i\sin\frac{17}{12}\pi\right) , \\[5pt]
& & 2 \left(\cos\frac{23}{12}\pi+i\sin\frac{23}{12}\pi\right)
\end{eqnarray}図で表せば、次のようになります。
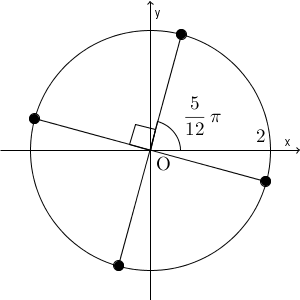
偏角については、同じ方向に4回回転して $\dfrac{5}{3}\pi$ になるものが、すべて解になります。
おわりに
ここでは、 $1$ 以外の複素数について、 $n$ 乗根を求める方法を見てきました。実部・虚部に分けて考えるよりも、絶対値と偏角に分けて考える、極形式を使ったほうが、ド・モアブルの定理のおかげで、計算しやすくなります。





