【基本】複素数の極形式

ここでは、複素数を、絶対値と角度を使って表す、極形式について見ていきます。

複素数の極形式

【基本】複素数平面の導入の後半で見たように、複素数 $i$ を掛けることは、複素数平面上で原点を中心に90度回転させることに対応してそうだ、ということを書きました。実は、複素数を掛けることは、回転と大きく関係しています。そのことを見越して、複素数を、角度を使って表す方法を見ていきます。

今まで、複素数 $\alpha$ の表し方は、実部と虚部に分けて、 $a+bi$ と書く方法を使ってきました。これは、複素数平面を、縦と横に切って考えているわけですね。

ここで、別の表し方を導入しましょう。まず、原点からの距離、つまり、絶対値を $r$ とします。式で書けば、\[ r=\sqrt{a^2+b^2} \]ということです。また、点 $r$ を原点を中心に $\theta$ だけ、反時計回りに回転したときに $\alpha$ と一致する、としましょう。

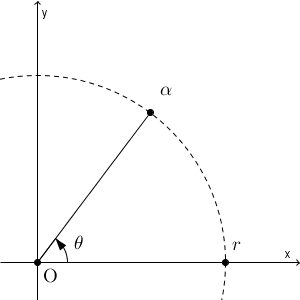
このとき、三角関数のときのことを思い出せば、 $a=r\cos\theta$, $b=r\sin\theta$ となります。よって、 $\alpha$ が $0$ でないときは、 $r$ と $\theta$ を使って、\[ \alpha=r(\cos \theta+i\sin\theta) \]と表すことができます。

$0$ でない複素数に対して、上のように表したものを、極形式(polar form) といいます。この $\theta$ のことを、偏角(argument) といい、 $\arg \alpha$ という記号で表します。偏角は、 $0\leqq \theta\lt 2\pi$ という条件を付ければ1つに決まりますが、一般には、 $2\pi$ の整数倍だけズレます。

$a+bi$ と表す方法は、複素数平面を縦と横に分けて考えていますが、極形式で表す方法は、原点からの距離と、実軸の正の向きとなす角で表しているので、次のように分けているイメージとなります。

$\cos\theta$ や $i\sin \theta$ の前につく符号がマイナスの場合は、プラスになるように偏角を調整します。具体的な計算を次で見てみましょう。

具体的に複素数の極形式を求めてみよう

複素数 $1+i$ の場合を考えます。まず、絶対値を求めてみると、\[ \sqrt{1^2+1^2}=\sqrt{2} \]となります。次に、偏角を考えましょう。 $\cos\theta=\dfrac{1}{\sqrt{2} }$, $\sin\theta=\dfrac{1}{\sqrt{2} }$ となる $\theta$ を考えると、\[ \theta=\dfrac{1}{4}\pi \]が見つかります。 $2\pi$ の整数だけ異なる角も条件を満たしますが、その中でわかりやすいものを選びます。以上より、\[ 1+i=\sqrt{2} \left(\cos\dfrac{1}{4}\pi +i\sin\frac{1}{4}\pi\right) \]が極形式で表したものとなります。

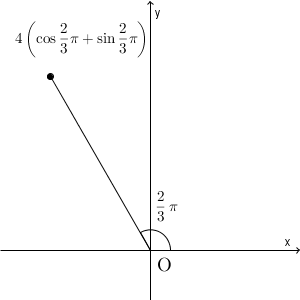
次に、 $-2+2\sqrt{3}i$ の場合を考えてみましょう。これも、まずは絶対値を考えます。\[ \sqrt{(-2)^2+(2\sqrt{3})^2}=4 \]となります。 $\cos\theta=-\dfrac{1}{2}$, $\sin\theta=\dfrac{\sqrt{3} }{2}$ となる $\theta$ を1つ探すと、 $\theta=\dfrac{2}{3}\pi$ なので、極形式で表したものは\[ 4\left(\cos\dfrac{2}{3}\pi +i\sin\frac{2}{3}\pi\right) \]となります。

これを図で表せば、次のようになります。

少し変わった形ですが、 $-\sqrt{2}$ の場合ならどうなるでしょうか。絶対値は $\sqrt{2}$ なので、 $\cos\theta=-1$, $\sin\theta=0$ となる $\theta$ を考えて、\[ \sqrt{2}\left(\cos\pi +i\sin\pi\right) \]となります。

共役複素数の極形式

$\alpha=r(\cos\theta+i\sin\theta)$ のとき、共役複素数 $\overline{\alpha}=r(\cos\theta-i\sin\theta)$ の極形式はどうなるでしょうか。 $i$ の前にある符号が、マイナスなので、プラスになるように偏角を調整しましょう。

この極形式を、式から考えるのは少し難しいですが、そもそも極形式がどういう決め方だったかを思い出せば、それほど難しくはありません。極形式を考えるには、まず絶対値を考えるのでした。共役複素数の絶対値は、もとの複素数の絶対値と同じですね。

絶対値を $r$ として、次に、点 $r$ をどのように回転すればいいかを考えましょう。

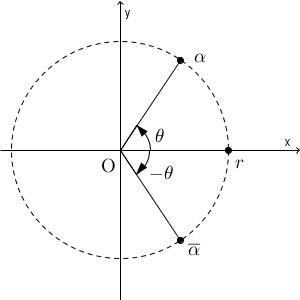
反時計回りに、 $\theta$ だけ回転すれば $\alpha$ となります。なので、共役複素数 $\overline{\alpha}$ と一致するには、反対向きに同じだけ回転すればいいので、偏角は $-\alpha$ となります。よって、共役複素数を極形式で表すと\[ \overline{\alpha}=r\{\cos(-\theta)+i\sin(-\theta)\} \]となります。

式で考えるなら、 $\cos\theta_1=\cos\theta$, $\sin\theta_1=-\sin\theta$ となる $\theta_1$ を考えることになりますが、共役複素数の図形的な意味から考えたほうが、おそらく簡単でしょう。

共役複素数の偏角は、元の複素数の偏角を $-1$ 倍したものなので、\[ \arg\overline{\alpha}=-\arg{\alpha} \]が成り立ちます。偏角の等式では、 $2\pi$ の整数倍の違いを除いて一致する、という意味です。

おわりに

ここでは、複素数を、絶対値と偏角を用いて表す、極形式について見てきました。この極形式を使うと、複素数の積や商が、回転と深く結びついていることがわかりやすくなります。