【基本】1のn乗根と極形式
ここでは、ド・モアブルの定理を用いて、1のn乗根を極形式で書くと、すごくシンプルに書けることを見ていきます。
1の3乗根
$1$ の $n$ 乗根について考える前に、まずは $n=3$ のとき、つまり、3乗根について考えてみましょう。
$x^3=1$ とすると
\begin{eqnarray}
x^3-1 &=& 0 \\[5pt]
(x-1)(x^2+x+1) &=& 0 \\[5pt]
\end{eqnarray}となるので、解は、\[ x = 1,\frac{-1\pm\sqrt{3}i}{2} \]となることがわかります。【基本】1の3乗根でも見ましたが、虚数解のうち、片方を $\omega$ と書くと、もう片方は $\omega^2$ と書けるのでした。
さて、これら3つの解を、極形式で書いてみると、次のようになります。
\begin{eqnarray}
1 &=& \cos 0+i\sin 0 \\[5pt]
\frac{-1+\sqrt{3}i}{2} &=& \cos \frac{2}{3}\pi+i\sin \frac{2}{3}\pi \\[5pt]
\frac{-1-\sqrt{3}i}{2} &=& \cos \frac{4}{3}\pi+i\sin \frac{4}{3}\pi \\[5pt]
\end{eqnarray}これを図でかくと、次のようになります。
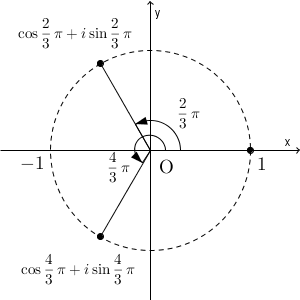
点 $1$ から出発して、 $\dfrac{2}{3}\pi$ ずつ回転した点が、 $1$ の3乗根に対応していることがわかります。
ド・モアブルの定理を使って計算すると、この結果はとても自然に感じられます。複素数 $z$ を極形式で表すと、
\[ z=r(\cos\theta+i\sin\theta) \]になるとしましょう。この3乗が $1$ になるとすれば\[ r^3(\cos3\theta+i\sin3\theta)=1 \]となります(参考:【基本】ド・モアブルの定理)。 $r$ は正の実数なので、 $r=1$ です。また、 $\theta$ は\[ 3\theta=2n\pi \]となればいいので、同じ複素数になるものを除くと、\[ \theta=0,\frac{2}{3}\pi,\frac{4}{3}\pi \]となることがわかります。
虚数解のうち、片方を $\omega$ と書くと、もう片方は $\omega^2$ となることも、極形式で考えれば簡単にチェックできますね。
1のn乗根
3乗根の場合を踏まえ、 $1$ の $n$ 乗根を同じように考えてみましょう( $n$ は正の整数)。
$z^n=1$ としましょう。 $|z|^n=|z^n|=1$ であり、 $|z|$ は正の実数だから、 $|z|=1$ となります。よって、\[
z=\cos\theta+i\sin\theta \]となることがわかります。ここで、ド・モアブルの定理から、\[ z^n=\cos n\theta+i\sin n \theta \]となります。これが $1$ と等しいので、 $n\theta$ は $2\pi$ の整数倍と等しいことがわかります。
このことから、整数 $k$ を使って、 $n\theta=2k\pi$ と表せることがわかります。これを変形すると、 $\theta=\dfrac{2k\pi}{n}$ となることから、\[ \cos\dfrac{2k\pi}{n}+i\sin\dfrac{2k\pi}{n} \]は、 $1$ の $n$ 乗根になります。これを $z_k$ と書くことにしましょう。
これらの点を、複素数平面上で考えてみましょう。
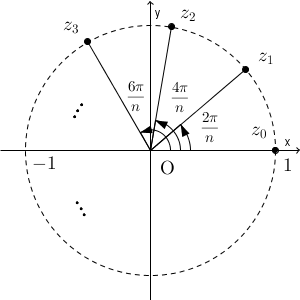
値を直接確かめても、上の図から考えても、どちらでもわかりますが、 $z_0$ から $z_{k-1}$ までは、すべて異なる値になります。それ以外は、この $n$ 個の値のどれかと一致してしまいます。よって、この $n$ 個の複素数が、 $1$ の $n$ 乗根となります。
例えば、 $1$ の6乗根なら、\[ \cos\dfrac{2k\pi}{6}+i\sin\dfrac{2k\pi}{6} \]なので、
\begin{eqnarray}
\pm 1,\ \pm\frac{1+\sqrt{3}i}{2},\ \pm\frac{-1+\sqrt{3}i}{2}
\end{eqnarray}となります。簡単に考えることができますね。

上の図を見れば、 $z_0$ から $z_{k-1}$ までの $n$ 個の点を結ぶと、正 $n$ 角形ができることがわかります。 $1$ の $n$ 乗根は、正 $n$ 角形(原点を中心とした半径 $1$ の円に内接し、点 $1$ を頂点に持つ)の頂点に対応する複素数だ、ということもできます。そのため、正 $n$ 角形を用いた問題で、 $n$ 乗根を利用することがあります。
おわりに
ここでは、ド・モアブルの定理を使って、 $1$ の $n$ 乗根について見ました。 $n$ 乗した結果が簡単に計算できるので、 $n$ 乗根も簡単に計算できるんですね。 $1$ 以外の数についても、 $n$ 乗根を計算することができますが、それはまた





