【基本】三角形の重心

🕒 2017/07/17 🔄 2023/08/20

ここでは、三角形の重心の性質について見ていきます。

📘 目次

中点連結定理

三角形の重心の話をする前に、中点連結定理の復習をしておきます。

線分のちょうど真ん中の点を、その線分の中点(midpoint) といいます。三角形 $\mathrm{ABC}$ について、辺 $\mathrm{AB,AC}$ の中点をそれぞれ $\mathrm{D,E}$ とします。

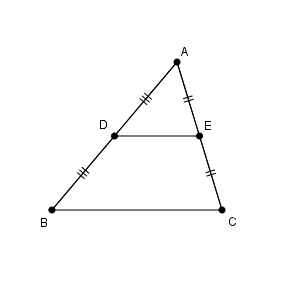
このとき、$\mathrm{ DE } /\!/ \mathrm{ BC }$ と、 $\mathrm{DE}=\dfrac{1}{2}\mathrm{BC}$ が成り立ちます。この内容を、中点連結定理(midpoint theorem) といいます。

証明もしておきましょう。 $\triangle \mathrm{ADE}$ と $\triangle \mathrm{ABC}$ について、\[ \mathrm{AD:AB}=\mathrm{AE:AC}=1:2 \]であることと $\angle \mathrm{A}$ が共通であることから、2組の辺の比とその間の角がそれぞれ等しいので、相似だとわかります。

よって、 $\angle \mathrm{ADE}=\angle \mathrm{ABC}$ より、$\mathrm{ DE } /\!/ \mathrm{ BC }$ がわかります。また、相似比が $1:2$ なので、 $\mathrm{DE}=\dfrac{1}{2}\mathrm{BC}$ もわかります。これで証明終わりです。

中点をつないだだけで成り立つので、いろんなところで活躍する定理です。

三角形の中線

三角形の重心の話をする前に、もう一つ、中線の話をしておきましょう。

三角形の頂点と、それに向かい合う辺の中点とを結んだ線分のことを中線(median) といいます。

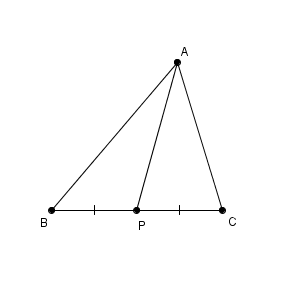
上の図で言うと、線分 AP が中線です。上の図では1つしかかいていませんが、中線は全部で3つあることがわかります。

三角形の中線の性質

三角形の中線について、次のような重要な性質があります。

三角形の中線の性質

三角形の3つの中線は1点で交わる。また、その点は、各中線を $2:1$ に内分する。

このことを示してみましょう。

まずは、各点に名前を付けて考えましょう。

三角形 ABC において、辺 BC, CA, AB の中点を、それぞれ P, Q, R とします。

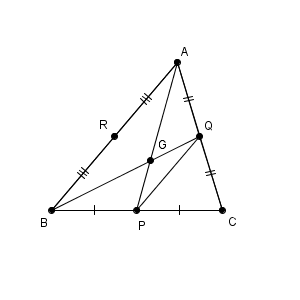
また、 AP, BQ の交点を G とおきます。この2つの中線は必ず交わります。というのも、 AP を基準にしたとき、 C は B とは違う領域にいます。そのため、 Q も B とは異なる領域にいます。よって、 BQ をつなぐと AP をまたぐしかないため、この2つの中線は必ず交わることになります。

注意が必要なのは、「 AP と BQ が交わる」「 AP と CR が交わる」はそれぞれすぐにわかりますが、この交点が一致するかどうかは明らかではない、ということです。ここで示そうとしているのは、この2点が実は一致しているということなんですね。

さて、中点といえば、先ほど示した「中点連結定理」が使えます。これより、 $\mathrm{ AB } /\!/ \mathrm{ PQ }$ がわかります。このことから、 $\triangle \mathrm{ ABG }$ と $\triangle \mathrm{ PQG }$ が相似であることがわかります。また、中点連結定理から $\mathrm{ AB }=2\mathrm{ PQ }$ なので、\[ \mathrm{ AG:GP } = \mathrm{ BG:GQ } = \mathrm{ AB:PQ } =2:1 \]であることがわかります。

次に、 AP と CR について考えましょう。この2つが交わることもすぐわかりますが、これが G と一致するかどうかはすぐにはわかりません。なので、この交点には別の名前 $\mathrm{ G }'$ をつけて考えましょう。

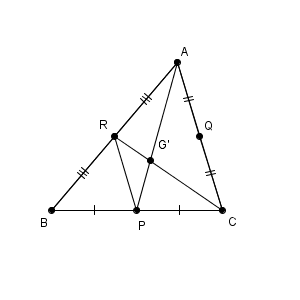
ただ、やることは同じです。先ほどと同じように中点連結定理を使えば、\[ \mathrm{ AG':G'P } = \mathrm{ CG':G'R } = \mathrm{ AC:PR } =2:1 \]であることがわかります。

この2つのことから、 $\mathrm{ G }$ も $\mathrm{ G' }$ も、 AP を $2:1$ に内分する点であることがわかるので、この2点は一致することがわかります。よって、3つの中線は1点で交わることがわかりました。

また、\[ \mathrm{ AG:GP } = \mathrm{ BG:GQ } = \mathrm{ CG:GR }=2:1 \]となることもわかるので、3つの中線の交点は、各中線を $2:1$ に内分することもわかります。

以上から、中線の性質が示せました。

三角形の重心

上で示した通り、三角形の3つの中線は1点で交わります。この点を三角形の重心(centroid) と呼びます。

「重心」というと、その点で釣り合うようなイメージがありますよね。実際、三角形が均質な同じ厚さの板でできていたとすると、3つの中線の交点で釣り合います。

正確にそのことを示すのは難しいですが、イメージとしてこう考えてみましょう。上の図の三角形 ABP と三角形 ACP は底辺と高さが同じなので、同じ面積です。なので、中線の両側は同じ重さになります。中線にそって三角形の板を乗せれば釣り合います。それらの交点は、釣り合う線の交点なので、やはり釣り合うとイメージできるでしょう。

また、こう考えることもできます。三角形自体の重さを無視して、 A, B, C に同じおもりをつけたとします。この3点が釣り合うポイントについて考えてみましょう。

このとき、 A から見れば、 B, C に同じおもりをつけるのと、この中点 P に2倍のおもりをつけるのは、同じ効果があるはずです。次に、 A と P とが釣り合うような場所を探せば、 AP を $2:1$ に内分する点が該当することがわかるでしょう。

ざっくりとした説明ですが、こうしたことから、3つの中線の交点を「重心」と呼ぶことが妥当であることがわかるのではないか、と思います。