【標準】三角形の外心・内心と角
ここでは、外心・内心の性質を使って角度を求める問題を見ていきます。
外心と角
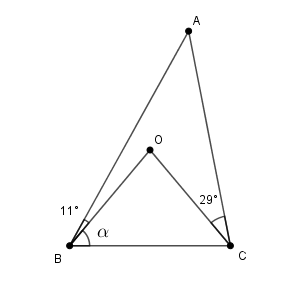
【基本】三角形の外心でも見た通り、外心とは外接円の中心のことであり、各辺の垂直二等分線が交わる点のことです。外接円とは、3つの頂点を通る円のことでした。
これを踏まえると、一般的には
- ・外心と各頂点を結ぶ
- ⇒線分が半径であることを使えるようになる
- ・外心から各辺に垂線をおろす
- ⇒垂線が各辺の中点を通ることを使えるようになる
- ・各頂点を通る円をかく
- ⇒円の性質が使えるようになる
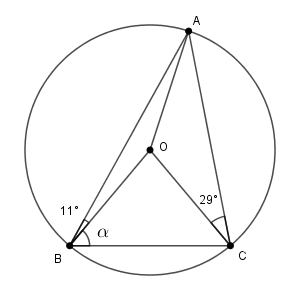
ここでは、外心と頂点を結び、円を追加しました。
このようにすれば、 $\mathrm{OA, OB, OC}$ は半径なので、$\triangle \mathrm{OAB}$, $\triangle \mathrm{OAC}$ は二等辺三角形です。なので、
\begin{eqnarray}
\angle \mathrm{BAC}
&=&
\angle \mathrm{BAO}+\angle \mathrm{CAO} \\[5pt]
&=&
\angle \mathrm{ABO}+\angle \mathrm{ACO} \\[5pt]
&=&
40^{\circ}
\end{eqnarray}とわかります。また、 $\angle \mathrm{BOC}$ は $\angle \mathrm{BAC}$ の中心角なので、\[ \angle \mathrm{BOC}=80^{\circ} \]となります。 $\triangle \mathrm{OBC}$ も二等辺三角形なので、\[ \alpha=\frac{180^{\circ}-80^{\circ}}{2}=50^{\circ} \]と求められます。
内心と角
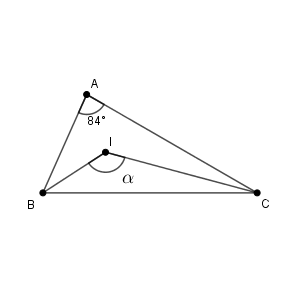
【基本】三角形の内心でも見た通り、内心とは内接円の中心のことであり、3つの角の二等分線が交わる点のことです。内接円とは、3つの辺に接する円のことでした。
これを踏まえると、一般的には
- ・内心と各頂点を結ぶ
- ⇒線分が角の二等分線であることを使えるようになる
- ・内心から各辺に垂線をおろす
- ⇒垂線の長さが等しいことを使えるようになる
- ・3つの辺に接する円をかく
- ⇒円や接線の性質が使えるようになる
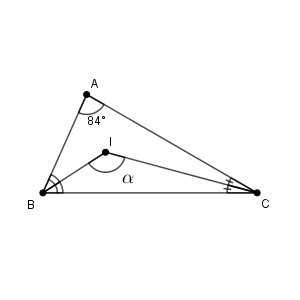
ただ、今の問題では、新しく線分や円を追加しなくても解くことができます。もともとある $\mathrm{IB, IC}$ が角の二等分線になっていることを使います。
$\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}$ はもちろん $180^{\circ}$ です。このことから、 $\angle \mathrm{B}, \angle \mathrm{C}$ の半分の角を足したものは\[ \frac{\angle \mathrm{B}+ \angle \mathrm{C}}{2}=\frac{180^{\circ} -\angle \mathrm{A}}{2}=48^{\circ} \]となります。 $\angle \mathrm{B}$ や $\angle \mathrm{C}$ の半分の値を直接求めることはできませんが、今の場合、和がわかればいいんですね。これを使うと、
\begin{eqnarray}
\alpha
&=&
180^{\circ}-(\angle \mathrm{IBC}+\angle \mathrm{ICB}) \\[5pt]
&=&
180^{\circ}-48^{\circ} \\[5pt]
&=&
132^{\circ}
\end{eqnarray}と求められます。
おわりに
ここでは、三角形の外心や内心の性質を使って、角を求める問題をみました。性質を使うために補助線を引いたり円を追加することもあります。





