【応用】三角関数の逆関数
ここでは、三角関数の逆関数を紹介していきます。
三角関数の逆関数を考える前に
関数 $f(x)$ の逆関数とは、 $y=f(x)$ としたときに $x=g(y)$ と書くことができる関数 $g(x)$ のことを言います(参考:【基本】逆関数)。
上のリンク先では、一次関数の逆関数が再び一次関数になることを見ました。また、【標準】指数関数の逆関数では、指数関数と対数関数が、互いに逆関数の関係になっていることを見ました。二次関数については、【基本】逆関数の定義域と値域で見たように、定義域を制限すれば、逆関数が考えられるようになり、逆関数は無理関数になることを見ました。
今までに出てきた関数に対して逆関数を考えてきましたが、ここでは、三角関数に対して考えてみましょう。
そもそも、三角関数の1つ $\sin x$ とは何だったかを思い出しておきましょう(参考:【基本】三角関数の定義)。これは、点 $(1,0)$ を、原点を中心として反時計回りに $x$ ラジアンだけ回転して移動した点の $y$ 座標を対応させるものでした。 $\cos x$ は $x$ 座標を、 $\tan x$ は、この移動後の点と原点とを結んだ直線の傾きを対応させるのでしたね。
下の図は、 $\theta$ に対して、 $\sin\theta$, $\cos\theta$, $\tan\theta$ をどう対応させるかを表したものです。
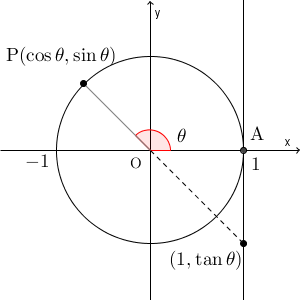
逆関数は、この逆の対応を与えるもの、となります。つまり、回転移動をした後の点の $y$ 座標に対して、回転した角を対応させるものが、「 $\sin$ の逆関数」となります。ただ、どう対応させるかを考えてみるとわかりますが、 $y$ 座標から角度を1つに決めることはできません。複数の角度が該当してしまいます。そのため、二次関数の逆関数を考えたときのように、値がかぶらないように、定義域を制限する必要があります。
以下では、定義域をどのように制限すれば、三角関数の逆関数が考えられるようになるかを見ていきます。
sinの逆関数
$y=\sin x$ のグラフをかいてみます(参考:【基本】三角関数のグラフ)。
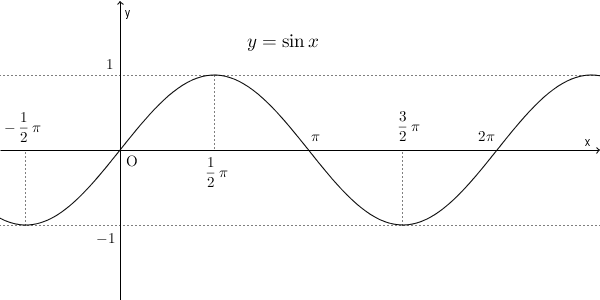
逆関数を考えるには、各 $y$ に対して1つの $x$ が対応するようになってないといけないので、範囲は、例えば、\[ -\dfrac{1}{2}\pi \leqq x \leqq \dfrac{1}{2}\pi \]にすればいいですね。こうすれば、 $y$ は $-1$ から $1$ までのすべての値を1回ずつ取るので、逆の対応を考えることができるようになります。(決め方は他にもありますが、以下ではこの範囲で考えます)
逆関数のグラフは、もとの関数のグラフと $y=x$ について対称なので、2つのグラフを合わせてかくと、次のようになります。

黒い曲線が $y=\sin x$ のグラフで、それを $y=x$ について対称移動したものが逆関数のグラフです。この逆関数は今までには出てきていない、新しい関数です。この関数には、 $\arcsin$ (アークサイン)という名前がついています。
この関数の名前にある、 arc についてコメントしておきましょう。arc とは、もともと「弧」という意味があります。先ほども書きましたが、 $\sin$ の逆関数は、「回転後の点の $y$ 座標から角度を対応させる関数」となります。ラジアンを用いた角度の表し方では、半径 $1$ の弧の長さと角度ラジアンは同じ数値になります(参考:【基本】弧度法)。なので、「回転後の点の $y$ 座標から、弧の長さを対応させる関数」と考えることもできます。こうした点から、 $\arcsin$ という名前がついています。
あとで、 $\cos$, $\tan$ の逆関数についても考えますが、これらの逆関数には、同様に、 $\arccos$, $\arctan$ という名前がついています。
cosの逆関数
$y=\cos x$ のグラフは次のようになります。
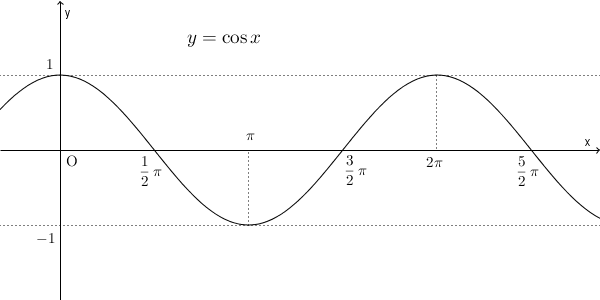
このときも、やはり、 $y$ から $x$ を決めるには、範囲を制限する必要があります。例えば、 $0\leqq x \leqq \pi$ とすればいいですね。この範囲では、 $y$ から $x$ をただ1つに決めることができます。他の範囲の取り方もありますが、この範囲で考えてみましょう。2つのグラフは次のようになります。

このようになります。 $y=\cos x$ の逆関数は、 $y=\arccos x$ と表します。アークコサイン、と呼びます。
tanの逆関数
$y=\tan x$ のグラフは次のようになります。
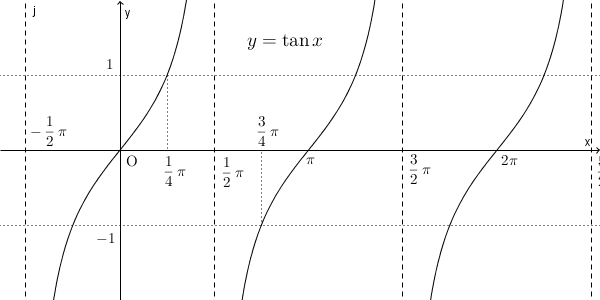
今までと少し形が違います。ただ、考えることは同じで、どのように制限をすれば $y$ から $x$ を1つに決めることができるか、です。グラフから、例えば、 $-\dfrac{\pi}{2}\leqq x \leqq \dfrac{\pi}{2}$ とすればいいことがわかるでしょう。2つのグラフをかくと、以下のようになります。
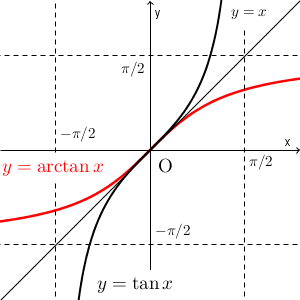
$y=\tan x$ の逆関数のグラフは上のようになります。 $y=\tan x$ の逆関数は、 $y=\arctan x$ と表します。アークタンジェント、といいます。
おわりに
ここでは、三角関数の逆関数の紹介をしました。ここで見た逆関数は、微分や積分の分野でまた登場するかもしれません。そのときに、またいろいろな性質を見ていくことになります。





