【標準】一次分数関数の逆関数

🕒 2018/07/10 🔄 2023/06/22

ここでは、逆関数を求める練習として、一次分数関数の逆関数を求めてみます。なお、一次分数関数は、【基本】一次分数関数で取り上げています。

📘 目次

一次分数関数の逆関数

次のような一次分数関数\[ f(x)=\dfrac{2x+1}{x+1} \]の逆関数を考えてみましょう。逆関数とは、 $y=f(x)$ が成り立つときに、 $x=g(y)$ が成り立つような関数 $g$ のことをいうのでした（参考：【基本】逆関数）。なので、 $y=f(x)$ とおいて、式変形をしていきましょう。

まず、関数 $f$ の値域について考えておきましょう。これが、逆関数の定義域にもなります。
\begin{eqnarray} f(x) &=& \frac{2x+1}{x+1} \\[5pt] &=& 2-\frac{1}{x+1} \\[5pt] \end{eqnarray}となります。 $\dfrac{1}{x+1}$ の部分は、0以外のすべての値をとります。よって、関数 $f$ の値域は、 $2$ 以外の実数全体、となります。

これを踏まえて、 $y=f(x)$ を変形し、 $x=$ の形にしてみましょう。
\begin{eqnarray} y &=& \frac{2x+1}{x+1} \\[5pt] (x+1)y &=& 2x+1 \\[5pt] xy-2x &=& 1-y \\[5pt] x &=& \frac{1-y}{y-2} \\[5pt] \end{eqnarray}このようになります。最後の式では、両辺を $y-2$ で割っていますが、値域が $2$ を含まないため、 $y-2$ が0になることはありません。なので、割ることができるのですね。

こうして、逆関数は、\[ f^{-1}(x)=\frac{1-x}{x-2} \]となることがわかります。

一次分数関数の逆関数のグラフ

逆関数を求めたので、今度はグラフについて考えてみましょう。

$f(x)$ のほうは、 $y=2-\dfrac{1}{x+1}$ と変形できることから、漸近線は、 $x=-1$ と $y=2$ となります。 $y=-\dfrac{1}{x}$ のグラフを平行移動したものになります。

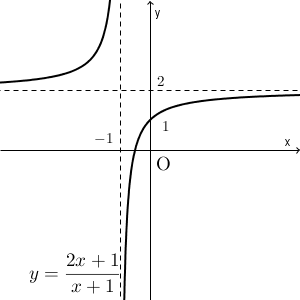
また、この逆関数の方は
\begin{eqnarray} y &=& \frac{1-x}{x-2} \\[5pt] &=& -1-\frac{1}{x-2} \\[5pt] \end{eqnarray}となるので、漸近線は、 $x=2$, $y=-1$ となります。また、 $y=-\dfrac{1}{x}$ のグラフを平行移動したものになります。

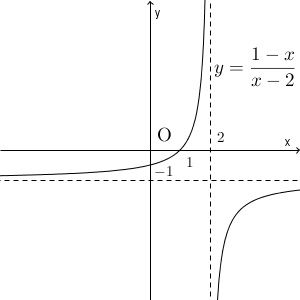
2つを並べてみましょう。元の関数と逆関数のグラフは、直線 $y=x$ について対称になることを見ました（参考：【基本】逆関数のグラフ）が、実際にそうなっていることがわかります。赤い方が逆関数です。

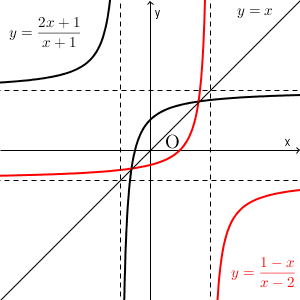
グラフ上の点だけでなく、2つの漸近線の交点なども直線 $y=x$ について対称となっていることがわかりますね。

【基本】一次分数関数で見たように、一次分数関数といったら、\[ y=\frac{ax+b}{cx+d} \]と書けるもののうち、 $c\ne 0$, $ad-bc\ne 0$ の場合を考えるのでした。もし $c=0$ ならただの一次関数だし、 $ad-bc=0$ なら約分ができて、定数関数になってしまうからです。

この一次分数関数のグラフは、双曲線 $y=\dfrac{k}{x}$ を平行移動したものになるのでしたね（参考：【基本】一次分数関数のグラフ）。逆関数のグラフは、この関数のグラフを直線 $y=x$ で対称移動したものだから、やはり双曲線となります。そのため、一次分数関数の逆関数は、一次分数関数になることが予想できます。

これらの予想は正しいのですが、別の機会にきちんと計算して確かめてみたいと思います。