【基本】逆関数のグラフ

ここでは、逆関数のグラフが、もとのグラフとどういう位置関係になるかを見ていきます。

逆関数の性質

ある関数 $f(x)$ に対して、逆関数 $f^{-1}(x)$ が存在するとします。

さて、 $a,b$ の間に次のような関係式があったとしましょう。\[ b=f(a) \]このとき、逆関数 $f^{-1}(x)$ というのは、この逆の対応を表すものだったので、\[ a=f^{-1}(b) \]が成り立ちます（参考：【基本】逆関数）。

例えば、 $f(x)=2x+4$ とすると、 $f^{-1}(x)=\dfrac{1}{2}x-2$ となります。求め方は上のリンク先にもありますが、 $y=f(x)$ を「 $x=$ 」の形に変形すればいいのでしたね。元の関数で、 $x=5$ とすると、 $f(5)=14$ となります。また、逆関数で $x=14$ とすると、 $f^{-1}(14)=5$ となります。逆関数は、もとの関数の逆の対応を表しているのだから、当然ですね。

逆関数のグラフ

【基本】逆関数の定義域と値域では、もとの関数と逆関数のグラフが、直線 $y=x$ について対称になっていることを見ました。ここでは、それがなぜ成り立つのかを考えてみましょう。

$y=f(x)$ のグラフ上の点 $(a,b)$ について考えてみましょう。 $y=f(x)$ のグラフ上にあるのだから、\[ b=f(a) \]が成り立ちます。

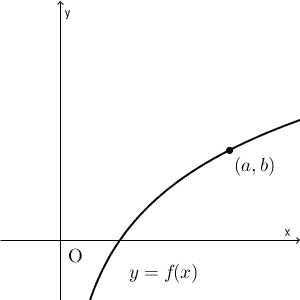
このとき、さきほど見た通り、逆関数の性質を使えば、 $a=f^{-1}(b)$ となることがわかります。よって、 $y=f^{-1}(x)$ で、 $x=b,y=a$ としたものが成り立つということですね。このことから、点 $(b,a)$ は、 $y=f^{-1}(x)$ のグラフ上にある、ということがわかります。

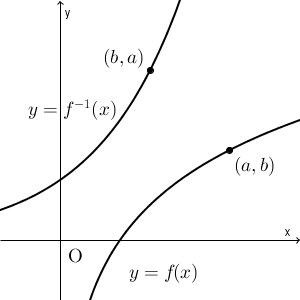
点 $(a,b)$ と点 $(b,a)$ は、直線 $y=x$ について対称です。 $y=f(x)$ 上のすべての点に対して、直線 $y=x$ について対称移動した点が $y=f^{-1}(x)$ 上にあることがわかり、逆に、 $y=f^{-1}(x)$ 上のすべての点に対して、直線 $y=x$ について対称移動した点が $y=f(x)$ 上にあることがわかります。

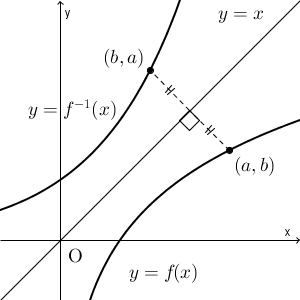
つまり、 $y=f(x)$ のグラフと $y=f^{-1}(x)$ のグラフは、直線 $y=x$ について対称であることがわかります。

上のリンク先からも確かめられますが、もとの関数の定義域に制限があった場合でも、もとの関数とその逆関数のグラフは、直線 $y=x$ について対称になります。

逆関数を求めるときに、 $x,y$ を入れ替えて求めましたが、このことと「直線 $y=x$ について対称であること」が対応しています。

おわりに

ここでは、逆関数のグラフの性質について見てきました。元の関数のグラフを $y=x$ について対称移動したものが、逆関数のグラフになります。