【基本】逆関数の定義域と値域
ここでは、逆関数の定義域と値域について考えます。ある関数の逆関数が存在しない場合でも、定義域を制限することで逆関数を考えられるようになることがあります。このような場合も含め、逆関数の定義域と値域について見ていきます。
定義域に制限のついた関数の逆関数
x, y が、ある関数 $f$ を使って $y=f(x)$ で表されるときに、逆に、 $x=g(y)$ を満たす関数 $g$ があれば、関数 $g$ は関数 $f$ の逆関数というのでした(参考:【基本】逆関数)。逆関数とは、逆の対応を表すもの、ということですね。逆関数は、 $f^{-1}(x)$ とも書きます。
上のリンク先では、縦が $2$ で 、横が $x$ の長方形に対し、周の長さを $y$ とした例を考えました。 x, y の間には、 $y=2x+4$, $x=\dfrac{1}{2}y-2$ という関係式が成り立ちます。なので、 $f(x)=2x+4$, $g(x)=\dfrac{1}{2}x-2$ とすると、 $g$ は $f$ の逆関数ということができます。
この関数を考えたときには特に定義域を制限しませんでしたが、長方形を考えるなら、本当は正であるという条件が付きます。以下では、さらに制限をつけて、 $2\lt x\leqq 5$ という条件を付けたときに、逆関数がどうなるかを考えてみましょう。
$y=f(x)=2x+4$ $(2\lt x\leqq 5)$ のグラフをかいてみると、次のようになります。
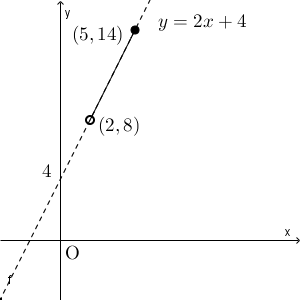
周の長さ $y$ の範囲は、グラフから、 $8\lt y \leqq 14$ となることがわかります。
では、この逆関数、つまり、周の長さから横の長さを対応させる関数を考えてみましょう。
まず、今考えている範囲では、周の長さは $8\lt y \leqq 14$ の間しか動きません。なので、逆関数の定義域(周の長さが取りうる値)は、この範囲となります。
この範囲で、周の長さから横の長さがどう対応するか、ですが、これは制限がなかったときと同じですね。逆関数の式自体が変わることはありません。
よって、この場合の逆関数は、 $g(x)=\dfrac{1}{2}x-2 \ (8\lt x \leqq 14)$ となります。ややこしいですが、関数の場合は一般に $x$ という変数を使うので、 $x$ に入れ替えています。
先ほどのグラフに、 $y=\dfrac{1}{2}x-2\ (8\lt x \leqq 14)$ のグラフを追加すると、次のようになります。
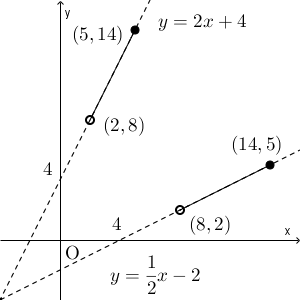
元の関数の値域が、逆関数の定義域になっています。また、元の関数の定義域が、逆関数の値域になっていることがわかります。
このグラフから、元の関数のグラフと、その逆関数のグラフは、直線 $y=x$ について対称になっていることがわかります。これは一般の場合にも成り立つのですが、このことについては、【基本】逆関数のグラフで詳しく見ていくことにします。
さて、ここまで見た内容を踏まえ、一般的に、逆関数の求め方を整理しておきましょう。
まず、 $y=f(x)$ の逆関数を考える場合は、 $x=g(y)$ の形に変形します。次に、 $x,y$ を入れ替えて、 $y=g(x)$ とすれば、これが逆関数になります。また、 $f(x)$ の値域が $g(x)$ の定義域となります。
定義域を制限することで逆関数が考えられる例
【基本】逆関数では、逆関数をもたない例も見ました。 $y=x^2$ としたとき、 $y=4$ に対応する $x=2,-2$ というように2つの値が対応してしまうため、逆関数が定義できないのでしたね。
逆関数が定義できない理由は、対応するものが複数あるからですが、逆にいえば、1つになるように元の関数の定義域を制限すれば、逆関数を考えられるようになります。
例えば、 $y=x^2\ (x\geqq 0)$ としてみましょう。 $x$ は0以上、 $y$ も0以上なので、 $x=\sqrt{y}$ と変形できます。よって、逆関数は、 $x,y$ を入れ替えた、 $y=\sqrt{x}$ になります。
2つのグラフをかいてみましょう。ちなみに、 $y=\sqrt{x}$ のグラフは、【基本】無理関数で扱っています。
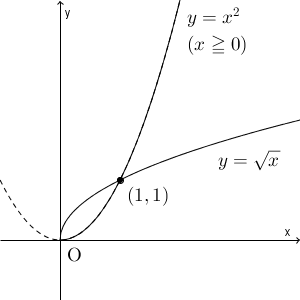
また、 $y=-x^2\ (x\leqq -1)$ としてみましょう。今度は $x,y$ は負なので、 $x=-\sqrt{-y}$ となり、値は1つに決まります。元の関数の値域は、 $y\leqq -1$ なので、 $x,y$ をすべて入れ替えて、逆関数は $y=-\sqrt{-x}\ (x\leqq -1)$ となります。グラフは次のようになります。
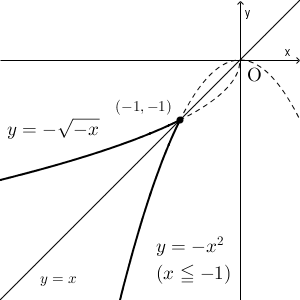
ちなみに、先ほども書きましたが、直線 $y=x$ について対称になっていることがわかりますね。
おわりに
ここでは、逆関数の定義域と値域について、見てきました。関数の値域が、逆関数の定義域になるのでしたね。また、関数の定義域を制限することで、逆関数が定義できるようになる例も見ました。





