【基本】三角関数の極限

ここでは、三角関数の極限に関する、重要な公式を見ていきます。

sinx÷xの極限

【基本】関数の極限とはさみうちの原理では、 $x\to\infty$ としたときの $\dfrac{\sin x}{x}$ の極限について考えました。分子は $-1$ から $1$ までの値しかとらない、ということを利用して、はさみうちの原理から、 $0$ に収束することが示せるのでした。

ここでは、 $x\to 0$ としたときの $\dfrac{\sin x}{x}$ の極限について考えてみましょう。分母も分子も $0$ に収束するので、そのままでは極限を考えることはできませんが、以下のようにして図形を用いて極限を考えることができます。

なお、角は弧度法で表されているとします（参考：【基本】弧度法）。

面積を使って考える

$x\to 0$ としたときの極限なので、 $x$ は $0$ に近い値だけを考えればいいですね。 $-\dfrac{\pi}{2}\lt x \lt \dfrac{\pi}{2}$ として考えていきます。

また、さらに、はじめは $0\lt x\lt \dfrac{\pi}{2}$ として考えていきます。負の場合は後で考えます。

弧度法とは、半径 $1$ の円の弧の長さを用いて角度を表す方法でした。1周なら $2\pi$ で、直角なら $\dfrac{\pi}{2}$ と表します。角が $x$ ならば、次の図のおうぎ形の弧の長さが $x$ ということです。

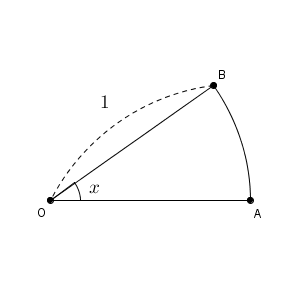
上の図は、点 O を中心とする半径 $1$ の円で、中心角が $x$ のおうぎ形 OAB です。このおうぎ形 OAB の面積は\[ \frac{1}{2}x \]となります（参考：【基本】弧度法を使ったおうぎ形の弧の長さと面積）。

さて、そもそも求めたかったのは $\dfrac{\sin x}{x}$ の極限でした。全然関係ないことを考えているように思えるかもしれませんが、上の図で B から OA に垂線を下ろせば、今考えたい極限の話につながってくることがわかります。

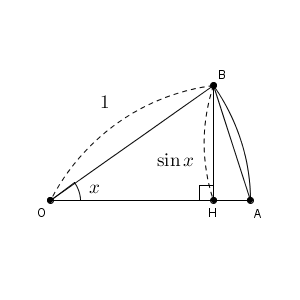
B から OA に引いた垂線の足を H とすると、 BH の長さは $\sin x$ となります。よって、三角形 OAB の面積は\[ \dfrac{1}{2}\sin x \]となります。また、おうぎ形の方が面積が大きいので、\[ \frac{1}{2}\sin x \lt \frac{1}{2}x \]が成り立ちます。今、 $x$ は正のときを考えているので、両辺を $\dfrac{1}{2}x$ で割れば、\[ \frac{\sin x}{x} \lt 1 \]となることがわかります。

ここで、もし、【基本】関数の極限とはさみうちの原理で見たように、はさみうちの原理が使えれば、 $\dfrac{\sin x}{x}$ の極限を求めることができそうです。式を見ていてもどうやってはさむかは思いつきにくいですが、さきほどの図で、おうぎ形をはさむことを考えてみるとどうでしょうか。

A を通り OA に垂直な直線と、直線OB との交点を C とします。このとき、 AC の長さは $\tan x$ となるので、三角形 OAC の面積は\[ \frac{1}{2}\tan x \]となります。これはおうぎ形の面積より大きいですね。また、三角関数の相互関係も使えば、
\begin{eqnarray} \frac{1}{2}x &\lt& \frac{1}{2} \tan x \\[5pt] x &\lt& \frac{\sin x}{\cos x} \\[5pt] \cos x &\lt& \frac{\sin x}{x} \\[5pt] \end{eqnarray}となります。 $0\lt x\lt \dfrac{\pi}{2}$ の範囲で考えているので、 $x$ も $\cos x$ も正なので、このような変形ができます。

以上から、 $0\lt x\lt \dfrac{\pi}{2}$ の範囲では\[ \cos x \lt \dfrac{\sin x}{x} \lt 1 \]が成り立ちます。 $x\to +0$ とすると、左辺は $1$ に収束するので、はさみうちの原理から\[ \lim_{x\to +0}\dfrac{\sin x}{x}=1 \]となることがわかります。

さて、最後に、 $-\dfrac{\pi}{2}\lt x\lt 0$ の場合を考え、 $x\to -0$ としたときの極限を求めましょう。この場合は、 $\theta=-x$ とすれば、
\begin{eqnarray} \lim_{x\to -0} \frac{\sin x}{x} &=& \lim_{\theta \to +0} \frac{\sin (-\theta)}{-\theta} \\[5pt] &=& \lim_{\theta \to +0} \frac{\sin \theta}{\theta} \\[5pt] &=& 1 \end{eqnarray}となります。対称性があるので、正の場合の結果を使いまわせるわけですね。

以上から、次の結論が得られました。

これは、弧度法でないと成り立ちません。度数法（1周を360°として角の大きさを表す方法）では、極限はこのようにはなりません。このきれいな結果を見れば、弧度法を使いたくなる気持ちもわかると思います。

おわりに

ここでは、三角関数の極限 $\displaystyle \lim_{x\to 0} \dfrac{\sin x}{x}=1$ について見てきました。今まで見てきた極限の計算とは異なり、式変形などでは示せません。面積を使ってはさみうちの原理を用いる、という証明方法は、あまり見ない手法です。証明方法まで覚えておく必要性は低いですが、この結果自体は今後とてもよく使います。