【基本】関数の極限

🕒 2018/08/18 🔄 2023/06/24

ここでは、関数の極限について見ていきます。

📘 目次

関数の極限（収束）

【基本】数列の極限では、数列 $\{a_n\}$ に対し、 $n\to\infty$ にしたときの極限を考えました。ある値 $\alpha$ に限りなく近づくなら、「収束する」といい、 $a_n\to\alpha$ などと書くのでした。また、それ以外は「発散する」というのでした。

関数についても「限りなく近づく」という極限の考えを導入することができます。数列の場合は、 $n\to\infty$ としましたが、関数の場合は少し異なります。具体的な関数で考えてみましょう。

$f(x)=\dfrac{2x^2-5x+2}{x-2}$ という関数を考えてみましょう。説明のために、少し人工的な例となっています。この関数は $x=2$ のところでは定義されませんが、それ以外のところでは定義されます。このグラフ $y=f(x)$ をかくと、次のようになります。

直線的ですね。それもそのはずで、この関数は次のように変形できるからです。
\begin{eqnarray} f(x) &=& \dfrac{2x^2-5x+2}{x-2} \\[5pt] &=& \dfrac{(x-2)(2x-1)}{x-2} \\[5pt] &=& 2x-1 \end{eqnarray}この関数では、 $x=2$ のときは定義されていませんが、 $x$ を $2$ に限りなく近づけていけば、 $f(x)$ は $2\times 2-1=3$ に限りなく近づいていくことがわかります。

このようにして、数列の極限を真似て、次のように関数の収束を考えます。

関数の極限（収束）

$x$ が $a$ 以外の値をとりながら $a$ に限りなく近づけたときに、関数 $f(x)$ がある値 $\alpha$ に限りなく近づくとする。このとき、「 $x$ が $a$ に近づくとき、 $f(x)$ は $\alpha$ に収束する」といい、この $\alpha$ のことを、極限値や極限と呼ぶ。このことを、次のような記号で表す。\[ \lim_{x\to a} f(x)=\alpha \]

「 $x$ が $a$ 以外の値をとりながら」というのは、 $x=a$ のまわりから近づけたときの値がどうなるかを考えたい、ということです。先ほどの例のように、 $x=a$ のときは定義されていなくてもいいし、定義されていても、極限値が $f(a)$ と異なる値となっていても構いません。

$\lim$ の記号を使わずに、「 $x\to a$ のとき $f(x)\to \alpha$ 」と書くこともあります。

関数の極限（収束しない）

数列の極限を考えたときは、収束することもありましたが、収束しないこともありました。関数の極限も同じです。収束しないこともあります。

例えば、 $f(x)=\dfrac{1}{x^2}$ という関数で、 $x\to 0$ としたときの極限を考えてみましょう。このグラフは次のようになります。

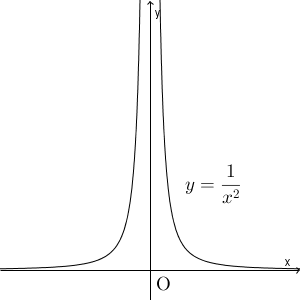
式を見てもわかる通り、 $x\to 0$ としたとき、 $f(x)$ は限りなく大きくなっていきます。

一般に、上のように、 $x$ を $a$ に限りなく近づけたとき、 $f(x)$ が限りなく大きくなる時は、「 $f(x)$ は正の無限大に発散する」といいます。\[ \lim_{x\to a}f(x)=\infty \]と書いたり、「 $x\to a$ のとき $f(x)\to \infty$ 」と書いたりします。

$f(x)$ が限りなく小さくなるとき（負で、絶対値が限りなく大きくなるとき）は、「負の無限大に発散する」といい、\[ \lim_{x\to a}f(x)=-\infty \]と書いたり、「 $x\to a$ のとき $f(x)\to -\infty$ 」と書いたりします。

収束もしないし、正の無限大にも負の無限大にも発散しない、という場合は、「極限はない」といいます。

例えば、 $f(x)=\dfrac{1}{x}$ で、 $x\to 0$ としたときを考えると、正の方から近づければ正の無限大に発散するし、負の方から近づければ負の無限大に発散してしまいます。近づけ方を変えると関数の値の近づく先が変わってしまい、値が1つに決まりません。このような場合に、「極限はない」といいます。