【基本】片側極限

🕒 2018/08/19 🔄 2023/06/24

ここでは、大きい方から近づけたり小さい方から近づけたときの極限について考えていきます。

📘 目次

片側極限

【基本】関数の極限でも見たように、 $x$ を $a$ に限りなく近づけたときに、 $f(x)$ の値が限りなくある値 $\alpha$ に近づくなら、 $f(x)$ は $\alpha$ に収束する、というのでした。また、限りなく大きくなったり、限りなく小さくなる（負で、絶対値が大）ときには、それぞれ、正の無限大に発散する、負の無限大に発散する、というのでした。

さらに、これら以外のケースがあることも見ました。例えば、 $f(x)=\dfrac{1}{x}$ の場合、 $x\to 0$ としたときは、正の値をとりながら $x$ を $0$ に近づけると、 $f(x)$ は正の無限大に発散します。負の値をとりながら近づけると、 $f(x)$ は負の無限大に発散します。このような場合には、「極限はない」というのでした。

極限がない場合でも、「 $x$ が $a$ より大きい値をとりながら限りなく近づける場合」に、 $f(x)$ がある値 $\alpha$ に近づいていくことがあります。このような場合、 $\alpha$ を右側極限(right limit) といい、次のような記号で表します。\[ \lim_{x\to a+0} f(x)=\alpha \]

また、「 $x$ が $a$ より小さい値をとりながら限りなく近づける場合」には、 $f(x)$ がある値 $\beta$ に近づいていく、という場合もあります。この場合は、 $\beta$ を左側極限(left limit) といい、次のような記号で表します。\[ \lim_{x\to a-0} f(x)=\alpha \]

この書き方通りに従えば、先ほどの $f(x)=\dfrac{1}{x}$ の場合、 $x\to 0$ としたときの極限は存在しませんが、右側極限は正の無限大、つまり、\[ \lim_{x\to 0+0} \dfrac{1}{x}=\infty \]となります。ただ、 $0+0$ の場合は、シンプルに $+0$ と書いて、\[ \lim_{x\to +0} \dfrac{1}{x}=\infty \]となります。左側極限は負の無限大であり、\[ \lim_{x\to -0} \dfrac{1}{x}=-\infty \]と表します。

「$x$ を、 $a$ より大きい値をとりながら限りなく近づける」ことを、「右から近づける」ということがあります。また、右側極限のことを「右側からの極限」ともいいます。

右側極限と左側極限を合わせて、片側極限(one-sided limit) といいます。

ガウス記号

片側極限の例としてよく挙がるのが、ガウス記号を使った関数です。ガウス記号とは、「その数を超えない、最大の整数を表す記号」のことです（参考：【標準】整数部分と小数部分）。

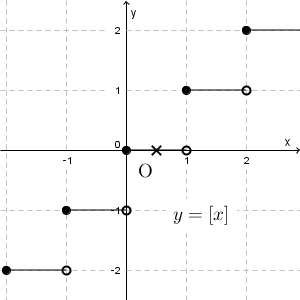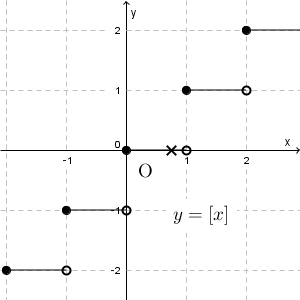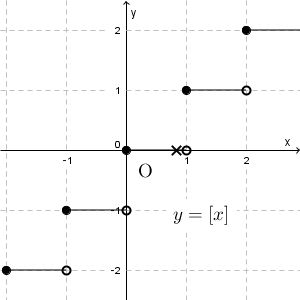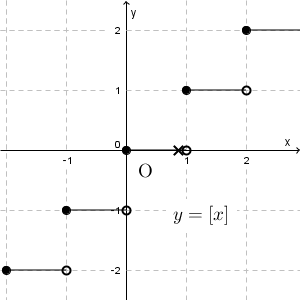
$x$ の整数部分を $\lbrack x\rbrack$ で表します。この $x$ のまわりにある記号がガウス記号です。 $f(x)= \lbrack x\rbrack$ とおいたとき、 $y=f(x)$ のグラフは、次のようになります。

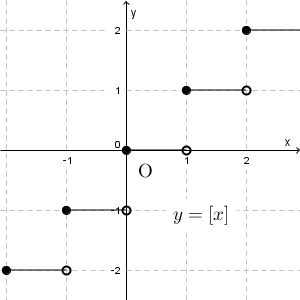
例えば、 $0\leqq x \lt 1$ のときは、 $x$ の整数部分は $0$ なので、この区間では $f(x)=\lbrack x\rbrack=0$ です。そして、 $x=1$ となった瞬間、整数部分は $1$ となり、 $1\leqq x \lt 2$ の間は、整数部分は変わらないので、 $f(x)=1$ となります。なので、上のようなグラフになります。

ここで、\[ \lim_{x\to 1+0} f(x) \]を考えてみましょう。この「 $1+0$ 」は、「1より大きい値をとりながら、 $x$ を1に近づけていく」ということを表していて、次のグラフの「×」の点の動きからもわかる通り、右側極限は1になることがわかります。

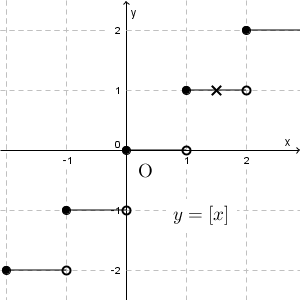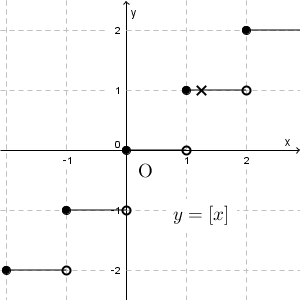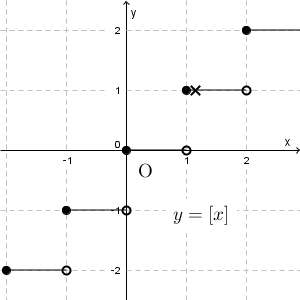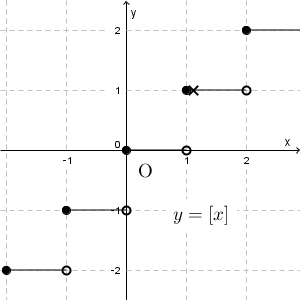
よって、\[ \lim_{x\to 1+0} f(x)=1 \]となります。

また、\[ \lim_{x\to 1-0} f(x) \]の場合は、「1より小さい値をとりながら、 $x$ を1に近づけていく」ということを表しています。 $0\leqq x \lt 1$ の間はずっと0なので、左側極限も $0$ となります。つまり、\[ \lim_{x\to 1-0} f(x)=0 \]となります。