【基本】対数関数の極限

🕒 2018/08/24 🔄 2023/05/01

ここでは、対数関数に関する極限について考えていきます。

📘 目次

対数関数の復習

対数関数の極限を考える前に、対数関数やそのグラフについて、少し復習しておきましょう。

【基本】対数で見たように、 $a$ が1でない正の実数で、 $a^p=M$ の関係があるときに、\[ p=\log_a M \]と書くのでした。 $a^p$ は正の数しかとらないので、 $M$ はつねに正の数になります。これを真数条件というのでした。

この $\log$ を使った、 $y=\log_a x$ を対数関数と呼びます。指数関数のグラフと同様に、底 $a$ によって対数関数のグラフは大きく形が変わってきます。【基本】対数関数のグラフや【基本】対数関数の性質でも見ましたが、もう一度見ておきましょう。

$a\gt 1$ のときは、 $y=\log_a x$ は、 $x$ が大きくなるほど大きくなります。

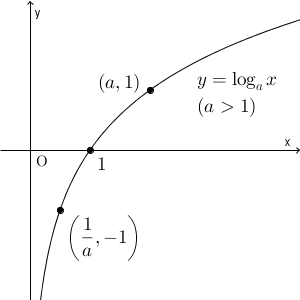
グラフは上のようになり、 $a\gt 1$ のときは、\[ \lim_{x\to\infty} \log_a x=\infty,\ \lim_{x\to +0} \log_a x=-\infty \]となります。 $y=\log_a x$ が成り立つことは、 $a^y=x$ が成り立つことと同じなので、 $x\to +0$ とすると、 $y\to -\infty$ となります。真数は正なので、右側極限しか考えられません（参考：【基本】片側極限）。

$0\lt a \lt 1$ のときは、 $y=\log_a x$ は、 $x$ が大きくなるほど小さくなります。

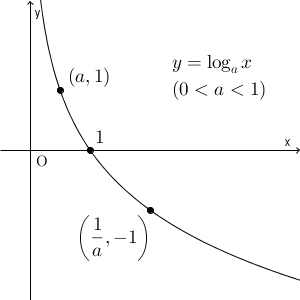
グラフは上のようになり、 $0\lt a \lt 1$ のときは、\[ \lim_{x\to\infty} \log_a x=-\infty,\ \lim_{x\to +0} \log_a x=\infty \]となります。

また、【標準】指数関数の逆関数で見たように、指数関数と対数関数は逆関数の関係になっており、グラフは、直線 $y=x$ について対称になります。

これらのことを思い出しつつ、対数関数の極限を考えていきましょう。

対数関数の極限（そのまま代入）

例題1

次の極限を求めなさい。\[ \lim_{x\to 1} \log_2 x \]

先ほどのグラフを見てもわかる通り、 $x\to 1$ とすると、 $\log_2 x$ は $\log_2 1$ に近づいていきます。よって、\[ \lim_{x\to 1} \log_2 x=0 \]となります。

定義域に含まれている場合は、そのまま代入するだけです。

対数関数の極限（真数をまとめる）

例題2

次の極限を求めなさい。\[ \lim_{x\to \infty} \{ \log_2 (2x-1)-\log_2 x \} \]

$x\to \infty$ とすると、2つの項はどちらも正の無限大に発散してしまいます。「∞ - ∞」となってしまうので、工夫して計算する必要があります。

対数の計算では、【基本】対数の性質（積や累乗の対数）で見たように、差を真数の商にまとめることができます。
\begin{eqnarray} & & \lim_{x\to \infty}\{ \log_2 (2x-1)-\log_2 x \} \\[5pt] &=& \lim_{x\to \infty} \log_2 \frac{2x-1}{x} \\[5pt] &=& \lim_{x\to \infty} \log_2 \left(2-\frac{1}{x}\right) \\[5pt] \end{eqnarray}となります。ここで、真数の部分は $2$ に収束するので、全体としては $\log_2 2=1$ に収束します。よって、\[ \lim_{x\to \infty} \{ \log_2 (2x-1)-\log_2 x \} = 1 \]となります。

対数関数の極限（因数分解を利用）

例題3

次の極限を求めなさい。\[ \lim_{x\to 1+0} \{ \log_2 (x^2-1)-\log_2 (x-1) \} \]

$x\to 1+0$ とすると、どちらの真数も、正の方から $0$ に近づいていきます。なので、どちらの項も、負の無限大に発散してしまいます。そのままでは計算できないので、先ほどと同じように真数をまとめて考えましょう。
\begin{eqnarray} & & \lim_{x\to 1+0} \{ \log_2 (x^2-1)-\log_2 (x-1) \} \\[5pt] &=& \lim_{x\to 1+0} \log_2 \frac{x^2-1}{x-1} \\[5pt] &=& \lim_{x\to 1+0} \log_2 \frac{(x-1)(x+1)}{x-1} \\[5pt] &=& \lim_{x\to 1+0} \log_2 (x+1) \\[5pt] \end{eqnarray}となります。分母・分子を $x-1$ で割ることで、分母・分子が $0$ に収束してしまうことを避けています。これにより、極限は $\log_2 2=1$ となることがわかります。\[ \lim_{x\to 1+0} \{ \log_2 (x^2-1)-\log_2 (x-1) \}=1 \]となります。