【基本】対数関数のグラフ

ここでは、対数関数のグラフがどうなるかを見ていきます。

log_2のグラフ

指数の場合は、まず、 $a^x$ の $x$ が自然数の場合、整数の場合、有理数の場合、実数の場合に、値がどうなるかを見ていき、それらを踏まえて、指数関数 $y=a^x$ のグラフがどうなるかを見ました（参考：【基本】指数関数のグラフ）。

対数の場合でも、 $\log_a M$ の値がどうなるか、どのように計算するかを見てきたので、対数関数 $y=\log_a x$ のグラフがどうなるかを見ていきます。

$a$ が1以外の正の数のとき、関数 $y=\log_a x$ を、 $a$ を底とする $x$ の対数関数(logarithmic function) といいます。なお、真数は正なので、 $x$ が正であること、つまり、定義域は正の実数全体であることに注意しましょう。

いきなり一般の場合を考えるのは難しいので、まずは具体的でシンプルな\[ y=\log_2 x \]について考えてみましょう。 $x=1,2,4,8$ を代入すれば、 $y=0,1,2,3$ であることがわかります。また、 $x=\dfrac{1}{2},\dfrac{1}{4}$ とすると、 $y=-1,-2$ となることがわかります。これらを踏まえて対応する点をとると、次のようになります。

$2^p\gt 2^q$ ならば $p\gt q$ なので、 $x$ が大きくなると、対数 $y=\log_2 x$ も大きくなる、つまり、グラフは右肩上がりになります。そのため、間をつなげていけば、 $y=\log_2 x$ のグラフが出来上がります。

$y=\log_2 x$ を変形すると、 $x=2^y$ となります。 $x$ を大きくしていくと $y$ はいくらでも大きくなります。また、 $x$ を0に近づけていくと、 $y$ はいくらでも小さくなっていきます。そのため、グラフの右上部分は、 $x$ 座標・ $y$ 座標はいくらでも大きくなっていき、左下の部分は、 $y$ 軸に近づいていきます。

指数関数との比較

先ほど、 $y=\log_2 x$ のグラフについて見ましたが、指数関数 $y=2^x$ のグラフと比較してみましょう。並べてかいてみます。

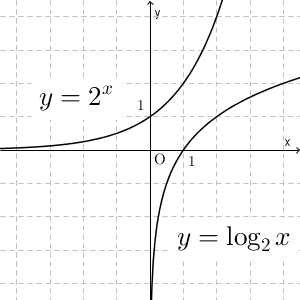
少し気づきにくいかもしれませんが、いくつか通る点を考えてみましょう。指数関数の方は、 $(0,1),(1,2),(2,4)$ といった点を通りますが、対数関数の方は、 $(1,0),(2,1),(4,2)$ といった点を通ります。 $x$ 座標と $y$ 座標が入れ替わっています。

これは偶然ではなく、対数関数の方を変形すれば当たり前であることがわかります。 $y=\log_2 x$ を変形すれば $x=2^y$ なので、 $y=2^x$ の $x,y$ を入れ替えたものになっています。なので、グラフ上の各点も、 $x$ 座標と $y$ 座標を入れ替えた点が対応します。

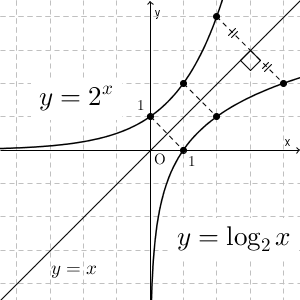
これより、対数関数のグラフと指数関数のグラフは、直線 $y=x$ について対称であることがわかります。 $(p,q)$ と $(q,p)$ について、中点が直線 $y=x$ にあり、2点を結ぶ直線の傾きが $-1$ であることからわかります。

他の対数関数のグラフ

先ほどの内容から、対数関数のグラフは、指数関数のグラフを直線 $y=x$ について対称移動したものだということがわかります。これを踏まえて指数関数のグラフを振り返ってみると、底によってグラフの形は大きく変わるのでした（参考：【基本】指数関数のグラフ）。

指数関数 $y=a^x$ の場合、グラフは $a$ の値によって変わります。1より大きければ、 $y=2^x$ のグラフのように右肩上がりになりますが、底が1より小さければ、次のように右肩下がりになります。

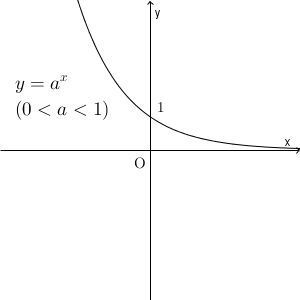
これを、直線 $y=x$ について対称移動したものが対数関数のグラフになるのでしたね。 $0\lt a \lt 1$ の場合、 $y=\log_2 x$ のグラフは、直線 $y=x$ で指数関数のグラフを反転させて、次のようになることがわかります。

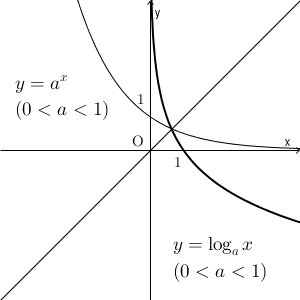
$a\gt 1$ のときと違って、グラフの左上の部分が $y$ 軸に近づいていくことがわかります。つまり、 $a$ の値によらず、対数関数のグラフは、 $y$ 軸が漸近線となることがわかります。

おわりに

ここでは、対数関数 $y=\log_2 x$ のグラフを見ました。底 $a$ が1より大きいか小さいかで、グラフの形が大きく変わることに注意しましょう。また、指数関数のグラフとの位置関係（直線 $y=x$ について対称であること）もおさえておきましょう。